גידול מעריכי
|
|
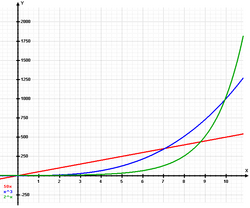
גידול מעריכי (באנגלית: Exponential growth) או גידול אקספוננטי או צמיחה מעריכית מתרחש כאשר קצב הגידול של תופעה כלשהי גדל בפרופורציה קבועה שתלויה בערך הנוכחי, לדוגמה קצב גידול של 3% בשנה. שם נוסף גידול כזה הוא גידול גאומטרי או טור גאומטרי. מודל הגידול המעריכי ידוע גם מודל צמיחה מלתוסיאני. למרות שקצב הגידול הוא קבוע פירוש הדבר שהגודל המוחלט של הנתון מכפיל את עצמו כל כמה פרקי זמן. לדוגמה אוכלוסייה שגדלה בקצב קבוע של 3% פירושו שהאוכלוסייה גדלה פי 2 בכל 25 שנה, לכן אם האוכלוסייה שומרת על קצב גידול קבוע, ומתחילה מגודל של 1 מיליון אז לאחר 25 שנה היא תמנה 2 מיליון איש, לאחר 50 שנה היא תמנה 4 מיליון איש, לאחר 75 שנה 8 מיליון איש וכך הלאה.
קיימות מספר תכונות של גידול מעריכי שהופכות את הטיפול בבעיות שגדלות בקצב מעריכי לקשות במיוחד. לדוגמה הערכות מערכות בריאות להתמודדות עם מגפה כמו קורונה היא קשה במיוחד עקב פחד מגידול מעריכי שיגרום לביקוש מהיר למשאבים של מערכת הבריאות כמו ציוד הנשמה ורופאים, עד לקריסת המערכת. החשש בקרב הוגים רבים בזרם הקיימות שבעיות עולמיות במספר תחומים שונות כמו אוכלוסין, זיהום, ניצול משאבי טבע או ניצול אנרגיה, יציבו אתגר גדול מידי לאנושות בגלל תכונות של גידול מעריכי שעלולות להיות להן.
דוגמאות מפורסמות לגידול מעריכי הן גידול של אוכלוסיית חיידקים, שמרים או חרקים בתוך בית גידול מבודד המכיל מזון, ואין בו גורמים מגבילים כמו טורפים או מחלות. לאוכלוסייה קצב גידול קבוע, המספק זמן הכפלה כלשהו. לאחר כל מחזור הכפלה גדלה האוכלוסייה פי 2. דבר זה נמשך עד אשר לבסוף האוכלוסייה מגיע לפיצוץ אוכלוסין שבעקבותיו היא גוועת ברעב או מרעילה את עצמה למוות בגלל חומרי פסולת שמצטברים. אפשרות אחרת היא מוות של חלק גדול מהאוכלוסייה כאשר חלק מהאוכלוסייה נכנס למצב של תרדמה או צאצאים במצב עמיד (כמו נבגים) בציפייה לשיפור עתידי בתנאים.
גידול מעריכי קשור ללולאת משוב מחזקת לדוגמה בהכפלת חיידקים, לולאת המשוב היא שבדור הבא יש לא רק יותר חיידקים אלא גם יותר חיידקים שמסוגלים להכפיל את עצמם. תהליכים מתמטיים שמתקיימים במישור המתמטי בלבד, יכולים לגדול באופן מעריכי. מספרים גדולים שבני אדם מתקשים לתפוס אותם (כמו גוגול או גוגולפלקס) הם נקודת ציון בתחילת הדרך עבור גידול מעריכי, שיכול להשיג כל מספר סופי בהינתן זמן מספיק וקצב הכפלה מספיק מהיר. לעומת זאת תהליכים טבעיים שמתרחשים במציאות תמיד דורשים נוכחות של חומר ואנרגיה ולכן הם כפופים לחוקי התרמודינמיקה שמגבילים בשלב מסויים את תהליך הגידול - בין אם בגלל מגבלה של מאסה, בגלל מגבלה של אנרגיה זמינה או בגלל מגבלות אחרות שהן ביטוי לקושי לשמור על ארגון עצמי. כך לדוגמה גידול חיידקים נראה כמו גידול מעריכי בשלב הראשון אבל בשלבים מאוחרים יותר נכנסות לולאות משוב מחלישות שמאטות את תהליך הגידול ועוצרות אותו לגמרי - בדרך כלל הסיבה בחיידקים היא גמר המזון הזמין להם או כניסה של גורם שמתחרה איתם על המזון או טורף אותם.
ככל הנראה, גידול אוכלוסיית העולם לא מקיים גידול מעריכי, בגלל שרמת הפריון של אישה ממוצעת יורדת עם השנים בכל מדינות העולם. כך שאוכלוסיית העולם האוכלוסייה תגדל ככל הנראה בצורת עקומה הדומה ל-S. עם זאת, בגלל גידול (אשר עוצמת הגידול עולה כל הזמן) בצריכת משאבים לנפש ובטביעת הרגל האקולוגית, משתנים רבים המתארים את ההשפעה המצטברת של בני האדם על הטבע - כמו הרס מערכות אקולוגיות, הכחדת מינים, צריכת משאבים מתכלים או התערבות במחזור החנקן עלולים להיות בעלי צמיחה מעריכית. ראו גבולות פלנטריים.
תכונות
חישוב מחזור ההכפלה מאחוז גידול תקופתי קבוע
מחזור הכפלה הוא כמות השנים שעוברת (או כמות התקופות שעוברת) שבה גודל מסויים גדל פי 2 או יותר. כלל אצבע המספק קירוב לאורך מחזור ההכפלה הוא חלוקת המספר 70 באחוז הגידול התקופתי. כך לדוגמה קצב גידול קבוע של 2% בשנה, נותן מחזור הכפלה של כ-35 שנה. קצב גידול קבוע של 3% נותן מחזור הכפלה של 25 שנה, קצב גידול של 7% בשנה, נותן מחזור הכפלה של 10 שנים, וקצב גידול של 10% נותן מחזור הכפלה של 7 שנים.
קצב גידול עצום ובלתי נתפס
מבחינה אינטואיטיבית לרוב בני האדם קשה מאוד לתפוס את המהירות של קצב גידול מעריכי. לדוגמה רוב האנשים מתקשים להעריך את סדר הגודל של מספר ההכפלות הדרושות כדי לבנות מגדל של שטרות בעובי מילימטר אחד שיגיע מכדור הארץ עד לירח (מרחק של 380,000 ק"מ) - 42 הכפלות.
גידול אוכלוסיית העולם - קצב גידול של 1.1 אחוז בשנה בקצב קבוע גורם לכך שהמאסה האנושית מגיעה למאסת הייקום הנצפה (כולל כל הכוכבים, הגלקסיות וכו') בתוך כ-10,000 שנה.
דחיסת כל ההיסטוריה לזמן הכפלה יחיד
הגידול במשך תקופת מחזור הכפלה בודד, שווה לגידול שהתרחש במשך כל ההיסטוריה שקדמה למחזור זה. לדוגמה, נדמיין כוכב לכת מסויים שבו זוג אנשים מתחיל שושלת שגדלה בקצב קבוע של 1% בשנה. נדרשות 2100 שנה כדי להגיע למיליארד איש (30 הכפלות * זמן מחזור הכפלה של 70 שנה). ידרשו רק 70 שנה נוספות כדי להוסיף עוד מיליארד תושבים לפלנטה זו.
קושי לתפוס את התופעה ולפעול מולה
בתופעות בעלות זמן הכפלה מהיר, קשה להבחין בתופעה שעלולה להיות בעייתית עד לשלב מאוחר מאוד שלה. דוגמה מפורסמת היא חבצלות מים שגדלות באגם ומכפילות את כמותן בכל שבוע. אם נניח שיתרחש אסון אקולוגי כאשר חבצלות המים יכסו 100% משטח האגם, עולה השאלה מתי יגלו בני אדם השוכנים לחוף האגם את קיום הבעיה, ויפעלו מולה. אם נניח שהם ערניים ומגלים את הבעיה כאשר חבצלות המים מכסות 6% משטח האגם, הדבר מעניק להם 4 שבועות בלבד להגיע להסכמה על מהות הבעיה ועל הדרך לפתור אותה. בגלל התכונה של גידול מעריכי, סך הגידול בתקופת ההכפלה האחרונה שווה לסך כל הגידול לפניו, פירוש הדבר שבעיות יכולות לצאת מכלל שליטה בצורה מהירה בלי שהדבר יתגלה אלא בשלב מאוחר מאוד.
שטח אגם הכינרת הוא 166 ק"מ רבועים או 166 מיליון מטרים רבועים. אם נניח ששטח כל שושנת מים הוא מטר אחד וזמן הכפלה של שבוע, יקח לשושנה בודדת 24 שבועות לכסות שטח של 8 קמ"ר שהם כ-6%, דבר זה משאיר 4 שבועות לכיסוי מלא של האגם בשושנות מים. דבר זה מחריף אם מניחים כי ייתכן גידול בקצב הגידול. אם נניח קצב הכפלה חודשי של השושנה, יקח לה יותר משנתיים להגיע לכיסוי של 8 קמ"ר. אם מסיבה כלשהי קצב הגידול עצמו גדל פי 4, כך שזמן ההכפלה חוזר להיות שבוע, יוותרו לתושבים 4 שבועות בלבד לטיפול בבעיה. בעיות סביבתיות רבות בעולם מאופיינות בגידול איטי מאוד במשך מיליוני שנים, ואז גידול בקצב ההכפלה במאות השנים האחרונות.
דוגמה להמחשה - גשר החיידקים אל השמש
ביולוגיה יכולה לתת דוגמה עד כמה גידול מעריכי הוא דבר שקשה לתפוס אותו, או להתמודד מולו:
נניח שיש לנו חיידק שמתרבה כל שעה. הוא משתכפל ונוצרים שני חיידקים באותו גודל. הגודל של חיידק בודד כזה הוא 3 מיקרו-מטר (מיליונית המטר). לכן צריך לשים 333 חיידקים צמודים זה לזה בשורה כדי ליצור פס חיידקים באורך מילימטר אחד. המרחק מכדור הארץ אל השמש הוא 150 מיליון ק"מ. כעבור כמה זמן של גידול בקצב קבוע - גידול מעריכי, של הכפלה כל שעה, יהיו לנו די חיידקים כדי שנוכל לבנות גשר של חיידקים בין כדור הארץ לשמש?
התשובה היא שתוך 56 שעות, כלומר יומיים ו-8 שעות, יוכלו חיידקים שיעמדו צמודים זה לזה להגיע למרחק של 260 מיליון ק"מ. די והותר כדי להגיע מכדור הארץ אל השמש.[1] להלן פירוט התשובה.
| הנתון | גודל | הערה |
| המרחק לשמש | 150,000,000 | 150 מיליון ק"מ |
| המרחק לשמש | 1.5E+14 | בתרגום למילימטרים |
| חיידק - 3 מיקרומטר | 0.003 | מילימטרים |
| אחרי 10 שעות | 3.072 | 3 מילימטר |
| אחרי 20 שעות | 3,145.728 | 3 מטרים |
| אחרי 30 שעות | 3,221,225.472 | 3 ק"מ |
| אחרי 40 שעות | 3298534883 | 3,000 ק"מ |
| אחרי 50 שעות | 3.3777E+12 | 3 מיליון ק"מ |
| אחרי 56 שעות | 2.16173E+14 | 260 מיליון ק"מ |
בתוך 5 שעות נוספות בלבד, כלומר תוך 61 שעות, שהן יומיים ו-13 שעות, מהזמן שבו היה לנו חיידק בודד, נוכל להקים "גשר חיידקים" מהשמש עד כוכב הלכת פלוטו שנמצא במרחק 6 מיליארד ק"מ ממנה. לשם השוואה, לחללית "ניו הורייזונס" ששוגרה בשנת 2006, ועברה ליד הירח כעבור 8 שעות מזמן השיגור, נדרשו 8 שנים כדי להגיע לקרבתו של פלוטו.[1] [1]
כדי ליצור גשר חיידקים מהשמש אל פרוקסימה קנטאורי, כוכב שנמצא במרחק 4 שנות אור, ידרשו לנו רק 74 שעות או שלושה ימים ושעתיים. כדי ליצור גשר חיידקים באורך גלקסיית שביל החלב, מרחק 100,000 שנות אור, ידרשו לחיידקים 89 שעות, שהם שלושה ימים ושעתיים (כמובן הדבר מתעלם מהמגבלה של מהירות האור, כפי שהתעלמנו ממגבלות אחרות כמו מציאת מקור אנרגיה לחיידקים ותנאי מחיה נוספים).[1]
אם נרצה ליצור ריבוע שכל צלע שלו היא באורך גלקסיית שביל החלב, ובעובי חיידק אחד, נבנה ראשית צלע מחיידקים באורך המתאים, ואז ניתן לכל חיידק בצלע להשתכפל לצדדים, כמו שעשה החיידק הראשון. הדבר יקח לחיידקים זמן כפול יחסית להקמת צלע החיידקים - כלומר 178 שעות שהם 7 ימים ו-10 שעות.[1]
לשם הקמת קובייה ענקית בעלת צלעות באורך גלקסיית שביל החלב, ידרש זמן גדול פי 3 יחסית להקמת צלע באורך הגלקסיה. קודם נבנה צלע, לאחר מכן ריבוע בעובי חיידק אחד ולבסוף ניתן לכל חיידק בריבוע להשתכפל וליצור גשר חיידקים באורך הגלקסיה על ציר העומק. הדבר ידרוש רק פי 3 זמן יחסית לצלע באורך הגלקסיה, כלומר 267 שעות, שהם 11 ימים ו-3 שעות. [1]
הדוגמאות האלה ממחישות כמה גידול מעריכי הוא דבר עצום - עם קצב השכפול המתאים, ועם הזנחה של מגבלות שונות על קצב גידול זה כמו מהירות האור או אנרגיה, אנחנו מצליחים להגיע מאחד הדברים הקטנים ביותר בקיום שלנו - חיידק שאנחנו לא מסוגלים לראות בכלל, לגלקסיה שהיא כה עצומה ביחס אלינו עד שידרשו לנו אלפי שנים להגיע להיקף שלה גם אם היינו יכולים לנסוע במהירות האור. דוגמה זו גם ממחישה מדוע גם בהינתן דבר קטן מאוד כמו חיידק, תהליכים טבעיים לאורך זמן בעצם גדלים לא בגידול מעריכי אלא כפונקציה דמויית S - שכן תמיד קיימת מגבלת משאבים שקיומה לא משמעותי בשלבים הראשונים של התהליך אבל הופכת להיות משמעותית יותר ויותר בשלבים מאוחרים יותר.
מגבלות על גידול מעריכי
גידול מעריכי אמיתי ניתן לתיאור רק במישור המתמטי הטהור הבנוי רק ממספרים. אפילו ביקום כזה, קשה לנו לתאר גידול מעריכי לאורך זמן. נוסחה מתמטית יכולה לתאר גידול מעריכי, אבל אם נרצה לתאר את הערכים המתקבלים מפונקציה מעריכית, נגיע לאחר זמן מה לערכים גבוהים מאוד שהתיאור המדוייק שלהם ידרוש משאבי טבע עצומים. דוגמה למספרים גדולים הם המספרים גוגול גוגולפלקס. הייצוג של המספר מיליארד במערכת מספרים עשרונית הוא 1 עם 9 אפסים אחריו. גוגול מיוצג על 1 עם מאה אפסים אחריו או עשר בחזקת 100. לשם השוואה - מעריכים שיש ביקום הנראה פחות מ 10 בחזקת חלקיקים יסודיים בודדים. גוגולפלקס הוא מספר גדול בהרבה והוא עשר בחזקת גוגל. כדי לכתוב את הייצוג העשרוני על נייר יש צורך להקיף את כדור הארץ מספר פעמים. למרות גודלם של מספרים אלה, כל תהליך של גידול מעריכי יעבור את המספרים האלה בשלב כלשהו ובהינתן זמן מספיק יגיע למספרים גדולים בהרבה.
בעולם המציאות כל העצמים מסביבו בנויים מאטומים, שבנויים מחלקיקים אלמנטריים, ולכן המגבלה התאורטית העליונה על תהליכים אלה היא מספר החלקיקים האלמנטריים בייקום הנצפה או עשר בחזקת 87. בדרך כלל קיימות מגבלות רבות נוספות. לדוגמה אם נניח שיש לנו תהליך שיכול לנצל את כל החומר ביקום, עדיין לוקח זמן להגיע אל כוכבים אחרים - מהירות האור היא מגבלה אחרת על גידול מעריכי - לכן לכל תהליך שמוגבל על ידי מהירות האור והוא מתחיל במערכת השמש תהיה מגבלת חומר של החומר הזמין במערכת השמש ולא יותר, רוב החומר הזמין האחר של היקום ימצא במרחק של 4 שנות אור לפחות מאיתנו. בנוסף - רוב המסה במערכת השמש נמצאת בשמש עצמה - מימן והליום בטמפרטורה של אלפי מעלות - תהליך שידרוש את מסה גדלה הולכת של חלקיקים יהיה מוגבל כנראה לחומר שניתן להפיק מכוכבי לכת. כמו כן רוב הדברים הדברים שאנו יכולים לגעת בהם לא עשויים רק ממימן - הם עשויים גם מיסודות אחרים כמו פחמן או זרחן שהכמות שלהם נמוכה בהרבה ממסת המימן במערכת השמש.
להלן מספר סדרי גודל למסה של גופים גדולים. מסת כדור הארץ היא 5.97×1024 קילוגרם, מסת השמש מסומנת לרוב ב- [math]\displaystyle{ M_{\odot} }[/math]. ומוערכת ב-1.9891x1030 קילוגרם. מסה זו גדולה בערך פי 330 אלף פעמים המסה של כדור הארץ. מסת גלקסיית שביל החלב מוערכת כיום כ-5.8x1011 מסות שמש, שהם כ-1.14x1042 קילוגרם. מסת הייקום הנצפה- שכוללת את כל מיליארדי הגלקסיות שאנו יכולים לצפות בהם כוללת מסה בגודל של כ-כ-1.5x1053 קילוגרם. לפי החוק הראשון של התרמודינמיקה, קיים שימור חומר-אנרגיה - כלומר לא ניתן ליצור חומר-אנרגיה יש מאין. כל תהליך הכולל עצמים פיזיים - כלומר כזה המערב בני אדם, חיידקים, צמחים, מחשבים, מכונות וכו' יהיה מוגבל לכל הפחות על ידי המסה העומדת לרשותנו.
מגבלות מציאותיות יותר של תהליכים טבעיים נובעים מהחוק השני של התרמודינמיקה. כל מערכת מעניינית מספיק - כמו וירוסים, חיידקים, מושבות חיידקים, בעלי חיים, צמחים, בני אדם, מחשבים, מכונות, ערים, מוסדות חברתיים היא מערכת שיש בה סדר פנימי כלשהו שחיוני לתפקוד שלה. כאשר סדר פנימי זה מפסיק להתקיים אנחנו מדברים על מוות של אותה מערכת. כדי לשמור על סדר פנימי זה יש צורך בהשקעה מתמדת של אקסרגיה - אנרגיה זמינה לעבודה, שלרוב מקורה הוא מהשמש (אנרגיה סולארית) או במערכות אנושיות במאות השנים האחרונות - מגלגול של אנרגיה זו בצורה של דלק מאובנים. המשותף לכל המערכות האלה הוא שהן סוג של מערכת דיאספטית שבה סדר פנימי דורש השקעה מתמקדת של אנרגיה שמתפזרת החוצה לאחר מכן כחום.
הגידול המעריכי לכאורה של תהליכים רבים קשור לקיום של לולאת משוב מחזקת ולשפע של חומרי גלם זמינים ואנרגיה שיכולה לתדלק הלאה את התהליך הנתון - לדוגמה לחיידקים בצלחת פטרי יש שפע של מאגרי מזון נתונים. ככל שאנחנו מתקדמים בתהליך הגידול, נכנסות עוד ועוד מגבלות על התהליך, או התחזקות של לולאת משוב מחלישה אחת לכל הפחות. לדוגמה המזון הזמין בצלחת הפטרי נגמר ומגביל את גידול החיידקים. אם נוכל להתעלם ממגבלה זו על ידי הזרמה מתמדת של מזון נוזלי לצלחת תכנס, מגבלה נוספת והיא מגבלת מקום. מגבלה אחרת יכולה להיות פינוי של פסולת, כניסה של טורפים או תחרות פנימית בין החיידקים בשאלה מי מהם יתרבה בקצב מהיר או יעיל יותר. אם נניח שמקום אינו מגבלה כלל - נניח חיידקים המסוגלים לגדול בחלל החיצון ולא בצלחת פטרי, נגלה שמגבלת המזון היא מגבלה קשה יותר ממה שחשבנו - שכן בסופו של דבר הפקת מזון זה תלויה באור השמש, וקצב הספקת המזון למושבת הענק של החיידקים תלוי בקצב זרימת אור השמש.
דוגמאות לגידול מעריכי בתחומים שונים
כל הדוגמאות הנ"ל, מלבד דוגמאות הנוגעות לחישובים מתמטיים תאורטיים, הם דברים שגדלים באופן מעריכי רק למשך זמן מסויים. לאחר זמן מה נכנסים לפעולה שיקולים נוספים - לולאות משוב נוספות שגורמות להאטת התהליך ולמעבר של המערכת לגידול סיגמואידי.
פיזיקה
- תגובת שרשרת גרעינית (עקרון היסוד מאחורי נשק גרעיני). כל גרעין אורניום שעובר ביקוע גרעיני פוגע במספר גרעינים אחרים וגורם לביקוע שלהם.
- שבירת מפולת שלגים בתוך חומר דיאלקטי. אלקטרון חופשי מקבל תאוצה מספקת על ידי שדה חשמלי חיצוני וכך הוא משחרר עוד אלקטרונים כשהוא פוגש בעוד אטומים או מולקולות בחומר הדיאלקטי. האלקטרונים הנוספים משחררים עוד אלקטרונים בגידול מעריכי. הדבר עשוי להוביל לשבירה דיאלקטית שלמה של החומר.
ביולוגיה
- מספר המיקרו-אורגניזמים שחיים בצלחת פטרי יגדל בצורה מעריכית עד לכילוי של חומר תזונתי חיוני. באופן כללי החיידק הראשון מתפצל ל-2 חיידקים, אלו מתחלקים ל-4 וכו', בדרך כלל הדבר נעשה בזמני התחלקות קבועים.
- נגיף (לדוגמה אבעבועות, סארס, קורונה וכו') מתפשט בדרך כלל בצורה מעריכית אם אין גורם מלאכותי (כמו חיסון או בידוד) שמגביל אותו. כל נשא של הנגיף יכול להדביק כמה אנשים חדשים.
- האוכלוסייה האנושית, אם מספר הלידות ומקרי המוות לאדם לשנה נשארת באותה רמה (ראו גם גידול לוגריתמי) - אם כי תרחיש זה אינו מדוייק - ראו בהמשך.
- תגובות רבות של יצורים חיים לגירויים, כולל תגובתיות בבני אדם, הם תגובות לוגריתמיות, שהן פונקציה הופכית לתגובה מעריכית. התדירות או העוצמה של קול לדוגמה נתפסים באופן לוגריתמי. גירוי לוגריתמי הוא הסיבה לכך שעצם שדרגת בהירותו גדלה באופן מעריכי נראה לנו כאילו הבהירות שלו גדלה באופן לינארי. לדרך תחושה והגבה זו יש הגיון הישרדותי. חשוב ליצור החי להגיב לטווח רחב של גירויים, בעוד שההבחנה המדוייקת בין עוצמות שונות היא חשובה פחות.
כלכלה
- שיווק רב שכבתי. רווח שגדל בצורה מעריכית הוא מה שמובטח למשתתפים למשווקים של מוצרים בעלי עקרון של שיווק רב שכבתי, כאשר כל אדם במורד השרשרת משווק את המוצר למספר אנשים. דבר דומה קיים ב"משחק פירמידה" או ב"משחק פונזי" שבהם יש רווחים גדולים למשקיעים הראשוניים והפסדים המתחלקים בין מספר רב של משתתפים שנכנסים בסוף המשחק.
- ריבית דריבית (Compound interest) מחילה את שער הריבית לא רק על הקרן אלה גם על הריבית עצמה. דבר זה בשער ריבית קבוע נותן החזר מעריכי להשקעה.
- מדעי המחשב
- כוח החישוב של מחשבים - הכפלת כוח החישוב של מחשבים בכל מספר שנים. דבר הידוע בשם חוק מור. קיימות מגבלות תאורטיות על יכולת החישוב של מחשבים לדוגמה - גם אם נדמיין מחשב מהיר מאד, מהירות התקשרות במחשב זה תהיה מוגבלת על ידי מהירות האור, והפעלתו תדרוש אנרגיה וחומר - דברים שיוצרים מגבלות של משאבים מצד אחד ושל העלאת הטמפרטורה הפנימית מצד שני.
- בתאוריה של סיבוכיות חישובים, אלגוריתמים שונים בעלי סיבוכיות מעריכית דורשים הגדלה מעריכית של משאבי חישוב (זכרון, זמן, מהירות מעבד) עבור גידול לינארי בגדולה של הבעיה. כך שבעיה שזמן הפתרון שלה עבור X=10 יהיה 10 שניות, תדרוש 20 שניות עבור X=11. אלגוריתמים אלה הופכים בדרך כלל לבלתי פתירים בגודל קטן מאוד - בין 30 ל-100 עצמים. מהר מאוד זמן החישוב הנדרש הופך להיות מיליארדי שנים.
- הגידול ברשת האינטרנט היה מעריכי, דוגמה לביקוש מושרה, וצפוי לעבור מתישהו לגידול בצורת S - בדומה לחדירת מוצרים רבים אחרים.
אוכלוסיית בני האדם
 ערך מורחב – גידול אוכלוסין
ערך מורחב – גידול אוכלוסין
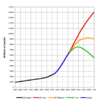
במציאות ייתכנו מצבים קיצוניים יותר מגידול מעריכי, אך ייתכנו גם מצבים מורכבים יותר. במשך רוב ההיסטוריה האנושית קצב הגידול של אוכלוסיית העולם היה בממוצע נמוך בהרבה מ-1% בגלל מגיפות, רעב, אסונות, מלחמות ומנגנונים של דעיכה או קריסה אקולוגית או כלכלית בתרבויות מקומיות. לקחו מספר מיליוני שנים עד שמספר בודד של בני אדם מסוג הומו-סאפינס התרבו לכדי כ-8 מיליוני בני אדם שחיו לפני כ-30,000 שנה כציידים לקטים שעברו את המהפכה הלשונית. מאז המהפכה החקלאית לפני 10,000 שנה, מספר בני האדם הלך וגדל מכמה מיליונים לכמיליארד בני אדם באזור שנת 1850. במאות השנים האחרונות גדל קצב הגידול של האוכלוסייה העולמית בעקבות שינויים כמו המהפכה התעשייתית, שיפורים ברפואה ובהיגיינה, שיפור התנובה החקלאית בגלל מספר מהפכות חקלאיות כמו המהפכה הירוקה ועוד שינויים טכנולוגיים. כך שב-1950 מספר בני האדם הגיע ל-2.5 מיליארד בני אדם. נתון זה קפץ לכ-7 מיליארד בני אדם בשנת 2000.
עם זאת, האוכלוסייה האנושית אינה גדלה בקצב מעריכי קבוע, ובדומה לעליה החדה בקצב הגידול, הייתה גם ירידה בקצב הגידול (שערכו שונה באזורים שונים בעולם), שההסבר המקובל לה הוא מעבר דמוגרפי. דבר זה אינו אומר שאוכלוסיית העולם היא בהכרח במגמת התייצבות, שכן למרות שכל אישה יולדת בממוצע פחות ילדים יש גם יותר נשים. תחזיות האו"ם להמשך גידול האוכלוסייה האנושית פתוחות למספר תרחישים שונים.
עם זאת, בגלל גידול גדל בצריכת משאבים לנפש ובטביעת הרגל האקולוגית, משתנים רבים המתארים את ההשפעה המצטברת של בני האדם על הטבע - כמו הרס מערכות אקולוגיות, הכחדת מינים, צריכת משאבים מתכלים או התערבות במחזור החנקן עלולים להיות בעלי צמיחה מעריכית או דומה לה שכן הם גדלים לא רק עקב גידול אוכלוסין אלא גם עקב צמיחה כלכלית בכל העולם, ושינויים בהרגלי הצריכה של מיליארדי אנשים שחיים במדינות מתפתחות. משתנים אלה מסוכמים לדוגמה במאמר גבולות פלנטריים.
ראו גם
- גבולות לצמיחה (ספר)
- התמוטטות (ספר)
- אריתמטיקה, אוכלוסייה, ואנרגיה (סרט)
- קורס בהתרסקות
- גבולות פלנטריים: חיפוש אחר נפח פעילות בטוח עבור האנושות (מאמר)
- שיא תפוקת הנפט
קישורים חיצוניים
- גידול מעריכי בוויקיפדיה האנגלית
- האם בני האדם חכמים יותר משמרים? סרטון ביוטיוב
- טלוויזיית ההחטאה מלמעלה הפקת סרטים תיעודיים להסבר על גידול מעריכי, כושר נשיאה, גלישה מלמעלה וקריסה
- ליה אטינגר, מה בין גידול מעריכי, קורונה ומשברים אקולוגיים, מרכז השל לקיימות, 6.9.2020
הערות שוליים
| אוכלוסין | |
|
מושגים: אוכלוסיית העולם - צפיפות אוכלוסין - צפיפות אוכלוסין פיזיולוגית - גידול אוכלוסין - מעבר דמוגרפי - גידול מעריכי - כושר נשיאה - המהפכה החקלאית - המהפכה הירוקה - ביטחון תזונתי - I=PAT - טביעת רגל אקולוגית - פיצוץ אוכלוסין - אסון מלתוסיאני - שיא תפוקת הנפט - ייצוב אוכלוסין - כלכלת מצב יציב |
|
|
סרטים וספרים: פצצת האוכלוסין - גבולות לצמיחה - התמוטטות - כלכלת מצב יציב - אריתמטיקה, אוכלוסייה ואנרגיה - תכנית ב' | |
|
גידול אוכלוסייה בישראל: אוכלוסיית ישראל - גידול אוכלוסיית ישראל - פריון הילודה בישראל - והארץ מלאה - הסיבות לעליית מחירי הדיור בישראל - פקקי תנועה בישראל - משק המים בישראל - הפורום לאוכלוסייה, סביבה וחברה | |
| מערכות מורכבות |
|
מושגי יסוד: הוליזם - שיווי משקל - תהליך - אנטרופיה - אקסרגיה - החוק השני של התרמודינמיקה - מידע - ארגון עצמי - הגחה - לולאת משוב - תהליך בלתי הפיך - עמידות - חשל - גידול מעריכי - תגובת יתר |
|
מערכות, מודלים וגישות: מערכת מורכבת - מערכת מפזרת - מודל מבוסס סוכנים - מערכת מורכבת אדפטיבית - חשיבה מערכתית - דינמיקה של מערכות - תורת המידע - כלכלה אבולוציונית - כלכלת מורכבות - שיטת המערכות הרכות |
|
מערכות ואקולוגיה: תהליך ארוך טווח - מחזור ביוגאוכימי - חוק המינימום של ליביג - פרדוקס ג'בונס - עקרון ההספק המקסימלי - הולון - אנרגיה גלומה - שירותי המערכת האקולוגית - ייצור ראשוני - מטבוליזם |
|
ספרים ומאמרים: ספינת החלל כדור הארץ - גבולות לצמיחה - מעבר לגבולות - חוק האנטרופיה והתהליך הכלכלי - תריסר נקודות מינוף להתערבות במערכת - דינמיקת מערכות פוגשת את העיתונות - עיצוב כלכלה הוליסטית לעולם בר קיימא |
|
אישים, הוגים וארגונים: דונאלה מדווז - ניקולס ג'ורג'סקיו-רוגן - האווארד ת. אודום - דיוויד בוהם - איליה פריגוז'ין - מכון סנטה פה |