שיווי משקל
שיווי משקל (באנגלית: Equilibrium) הוא מונח הנוגע למערכות בתחומים שונים, המציין מצב של העדר שינוי בחלק מהתכונות של המערכת. בכך, שיווי משקל הוא כביכול ניגודו של תהליך, אם כי במקרים רבים שיווי משקל מציין תהליך דינמי אשר יש לו מימדים שבהם אין שינוי לאורך תקופה מסויימת.
שיווי המשקל הידוע והמקובל ביותר הוא שיווי משקל מכאני - מערכת פיזיקלית שבה שקול הכוחות ושקול המומנטים בכל נקודה במערכת שווים לאפס - לדוגמה אדם ההולך על חבל, סביבון מסתובב, או מאזניים (מאוזנים או בלתי מאוזנים).
יציבות של שיווי משקל
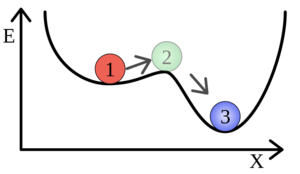
מאפיין חשוב של שיווי המשקל הוא עד כמה הוא יציב.
- שיווי משקל יציב הוא שיווי משקל שבו שינוי קטן שמופעל על המערכת או בתוכה, יצור תנודה קטנה סביב נקודת שווי המשקל (למשל כדור שמונח בתוך קערה עגולה), והמערכת תחזור לאותה נקודה שבה התחילה. במונחים של חשבון אינפיניטסימלי זהו מינימום מקומי של האנרגיה.
- שיווי משקל לא יציב או שיווי משקל רופף הוא שיווי משקל שבו שינוי קטן במערכת יוביל להתרחקות מנקודת שיווי המשקל הקודמת. במערכת מכאנית - תנועה קלה בכיוון כלשהו תגרום לכוחות הפועלים על גוף להוציאו משיווי משקל (למשל כדור שנמצא בראש גבעה או קערה עגולה הפוכה), והוא מקסימום מקומי של האנרגיה.
- שיווי משקל אדיש הוא מצב שבו תנועה קלה תמשיך ללא שינוי משמעותי, ובו הנגזרת של האנרגיה מתאפסת למשך כל התנועה. במערכת מכאנית הדבר דומה לכדור הנמצא על משטח ישר ומאוזן - אם נזיז את הכדור 10 ס"מ ימינה הוא יישאר שם ולא יעבור לנקודת שיווי משקל אחרת. אם ניתן לו דחיפה קלה אז בהנחה של חוסר חיכוך הכדור ימשיך לנוע על גבי המשטח.
שיווי משקל מכני אינו מעיד בהכרח על סטטיות - גוף קשיח השרוי בשיווי משקל אינו מצוי תחת תאוצה קווית או רדיאלית, אך ייתכן שיתמיד בתנועה קודמת (שילוב של מהירות קווית או מהירות זוויתית קבועה) שהוקנתה לו בטרם היה בשיווי משקל - לדוגמה סביבון שמסתובב (בעל תנועה מעגלית קבועה) או רוכב אופניים (בעל מהירות קווית קבועה). שיווי משקל סטטי הוא מקרה פרטי של שיווי משקל מכני המתקיים בגופים סטטיים. נאמר שמתקיים שיווי משקל סטטי כאשר מערכת כוחות המופעלת על גוף אינה מייצרת תנועה.
בתרמודינמיקה מבחינים בין שיווי משקל לבין מצב יציב. שיווי משקל תרמודינמי הוא מצב שבו אין זרימה של חום בין שני מאגרים. לעומת זאת "מצב יציב" הוא מצב שבו תיתכן זרימה של חום בין שני רכיבים במערכת, אבל הזרימה הזאת יציבה ולא משתנה על פני זמן. כל שיווי משקל תרמודינמי הוא גם מצב-יציב (עם זרימה אפס) אבל ייתכנו מצבים רבים שהם מצב יציב שאינם שיווי משקל תרמודינמי. מצב יציב זה אינו קשור ליציבות של שיווי המשקל. ייתכן ואנו נמצאים ב"מצב יציב" שבו יש שיווי משקל, אבל שינוי קטן של המערכת יגרור שינוי מהותי בשיווי המשקל.
בביולוגיה, אקולוגיה, פסיכולוגיה, כלכלה אקולוגית ובתחומים נוספים של מערכות מורכבות כגון מערכות צבאיות, מבחינים בתכונות נוספות של מערכות הקשורות ליציבות של שיווי משקל - רובסטיות ועמידות. רובסטיות (Robustness) היא תכונה של מערכת מפזרת המגדילה את הסיכוי של המערכת לשמור על המבנה והתפקוד שלה למרות שינויים בנסיבות, או כוח חיצוני, שמשנה את הפרמטרים של הנישה שבה המערכת נמצאת. היא יכולה להיות מוגדרת גם בתור אי-רגישות של מודל לשינויים קטנים בתנאי הסביבה. עמידות (Resilience) או גמישות-מערכתית היא מונח דומה המתאר את מידת היכולת של מערכת לשוב לשיווי משקל "בריא" בעל תפקוד גבוה לאחר הפרעה כלשהי.
שיווי-משקל יחיד או מרובה, והימצאות באי-שיווי-משקל
יש מערכות בהן יש שיווי משקל יחיד, כלומר מערכת שלא משנה מה יהיו תנאי ההתחלה שלה היא תמיד תגיע בסופו של דבר לאותו נקודה. לדוגמה, אם ניקח כדור ונזרוק אותו בכל נקודה בבקעה חלקה דמויית קערה, בכל מקום שנשחרר אותו הכדור תמיד יגיע לאותה נקודה בדיוק. זהו שיווי משקל יחיד. שיווי משקל יחיד הוא בהכרח גם שיווי משקל יציב שכן אם נזיז את הכדור מנקודת שיווי המשקל יהיו כוחות שיחזירו את המערכת לנקודת שיווי המשקל בצורה ספונטנית.
בתחום של מערכות מורכבות ומערכות דינמיות, ריבוי נקודות שיווי משקל (Multistability) היא תכונה של המערכת של קיום מספר נקודות שיווי משקל יציבות. על פי חוקי מתמטיים בגלל ששתי נקודות יציבות כאלה נמצאות במרחב רב-מימדי מסויים (שנפרס על ידי כל האפשרויות של משתנים המשפיעים על המערכת) חייבות להתקיים בין נקודות אלה גם נקודות עם שיווי משקל בלתי-יציב. נקודות שהן יציבות במימדים מסויימים של המערכת אבל לא יציבות במימדים אחרים, נחשבות כנקודות לא יציבות.[1]
ברוב המערכות הקיימות בעולם האמיתי, אין שיווי משקל יחיד, אלא ריבוי נקודות שיווי משקל - כלומר מספר מצבים בהם המערכת מסוגלת להימצא. לרוב יש במערכות אלה נקודות שיווי משקל יציבות ובלתי יציבות וכן שיווי משקל יציבים באופן מקומי. לדוגמה נתונה בקעה עמוקה שיש בה ערוצים שונים, שיחים וכו'. אם נשחרר בה כדור הוא לא בהכרח יגיע לנקודה הנמוכה ביותר בבקעה זו. אם הוא נתקע בערוץ מקומי הוא נמצא בנקודת שיווי משקל מקומי או "מינימום מקומי". בסיכוי קטן ייתכן שהכדור נמצא בראש גבעה קטנה ואז הוא בשיווי משקל מקומי בלתי יציב, התערבות כלשהי באחת מנקודות שיווי משקל אלה עשויה לגרום לכדור לעבור לנקודת שיווי משקל מקומית אחרת או לנקודת שיווי משקל כללית. מצב שבו הבקעה מחולקת לשתי גאיות עמוקים תיצור 2 נקודות שיווי משקל כלליות ויציבות, ולפחות נקודת שיווי משקל אחת בלתי-יציבה ביניהן.
כאשר למערכת יש מספר שיווי משקל, עצם זה שהם קיימים לא מחייב שהמערכת נמצאת באמת באחד מהם או שהיא קרובה לאחד מהם. יש מערכות מורכבת (כמו הפרפר של לורנץ) בהן סביר שהמערכת תתקיים יותר זמן באי-שיווי-משקל מאשר בשיווי משקל. המערכת מתנדנדת סביב נקודות שיווי המשקל כאשר כל אחת מושכת לכיוונה. אין שום הבטחה שיציאה משיווי משקל תהיה למשך זמן קצר או ל"מרחק" קצר (כלומר ששיווי המשקל יהיה יציב). רעיון זה בוטא בזמנו בכלכלה על ידי ג'ון מיינרד קיינס ("בטווח הארוך נהיה כולנו מתים"), והוא מתאים להתנהגות של מערכת תרמודינמית - שהיא מעניינת (או מבצעת עבודה) כל עוד היא נמצאת מחוץ לשיווי משקל תרמודינמי.
מערכת יכולה להיות מערכת מסודרת או מערכת שנראית "כאוטית" אם זאת מערכת כאוטית אינה בעלת אי-סדר מוחלט, אלא התנהגות חסומה; כלומר, מוגבלת לאירועים מסוימים, ושואפת למושך (פיזיקה) – אוסף יציב של מצבים. מושכים שונים הם :
- ההתכנסות לנקודת איזון (אקוויליבריום - שיווי משקל) - לדוגמה כדור הנמצא בתחתית של כד.
- ההתכנסות למסלול מחזורי - לדוגמה כדור הארץ הנע סביב השמש.
- ההתכנסות למסלול כמעט מחזורי
- מושך מוזר; מסלול שהמערכת מתכנסת אליו, בעל אופי פרקטלי לודגמה "הפרפר של לונרץ" במערכות מסויימות בעלות 3 משתנים - המערכת נעה בצורה מחזורית סביב נקודה מסויימת ואז בשינוי קטן מאד של התנעים עוברת לנוע לתנועה כמו-מחזורית סביב מסלול אחר. גם ממנו היא עשויה לחזור לשיווי משקל הראשון בעקבות שינוי קטן מאד בתנאים. צורה זו של מושך נוספה על ידי תורת הכאוס.
שיווי משקל יציב מקומית ומערכות ביולוגיות
שיווי משקל יציב או לא יציב בצורה גלובלית הם מקרים נדירים יחסית בטבע. לרוב נתקלים במערכות שיש בהן נקודות של שיווי משקל יציב מקומי - כלומר נקודות שבהן יש מידה מסויימת של יציבות, אבל רק עד גודל מסויים של הפרעה.
לדוגמה כדור בתוך קערה הוא למעשה שיווי משקל יציב באופן מקומי - דחיפה חזקה מדי תעיף אותו מחוץ לקערה. רוב המערכות הביולוגיות והחברתיות הן מערכות בעלות שיווי משקל יציב מקומית - יש בהן לולאות משוב מחלישות שדוחפות את המערכת חזרה לשיווי משקל, אבל התערבות חזקה מידי, או לחץ מתמשך עשויים לגרום לשינוי בלתי הפיך ומעבר לשיווי משקל אחר - לרוב לשיווי משקל פחות רצוי.
לדוגמה הומאוסטזה - שיווי משקל כימי ותרמודינמי פנימי בגוף חי המאפשר לגוף להמשיך לחיות (למעשה מדובר במצב יציב מבחינה תרמודינמית שכן יש זרימה מתמדת של אנרגיה דרך הגוף והחוצה). זהו תהליך בעל שיווי משקל יציב באופן מקומי - הגוף בנוי כך שהוא יכול להתמודד עם פציעות ועם מחלות ובעיות אחרות כל עוד הן מספיק חלשות, אבל פציעה במקום אסטרטגי או חזקה מידי או פגיעה בגוף לאחר שכבר התרחק ממצב של שיווי משקל זה (לדוגמה מחסור בחמצן עבור חולה לב, מחלה אחת בעקבות אחרת וכו') תגרום לאובדן שיווי המשקל ולהתדרדרות או למצב חדש של נכות או תת-תפקוד גופני יציב כלשהו, או עד למוות - שהוא גם סוג של שיווי משקל אחר של הגוף (שבו אין חילופי חומרים כימיים, ואין שינוי תרמודינמי). מוות הוא שיווי משקל יציב מבחינה גלובלית ואף תוצאה של תהליך בלתי הפיך.
גם מערכת אקולוגית נמצאת רוב הזמן בשיווי משקל מקומי או מסביב לשיווי משקל מקומי כזה - היא יכולה לסבול הפרעה או שינוי בגודל נתון - לדוגמה כניסה של מין פולש, הכחדה של אחד המינים, הפחתה בכמות המשקעים, זיהום, סופה, בירוא יערות, סחף קרקע, שריפה, קיטוע שטחי מחייה ועוד. הפרעה חזקה מידי או הפרעות חוזרות ונשנות עלולות לגרום לשינוי כולל של המערכת האקולוגית או לקריסה כוללת שלה - כלומר מצב שבו כלל המינים השותפים במערכת האקולוגית לא מסוגלים עוד להתקיים באותו איזור בגלל העדר נישות אקולוגיות מתאימות - עליהן לנדוד למקום אחר או להיכחד, והמערכת האקולוגית עצמה לא מתקיימת יותר או שהיא מפנה את מקומה לסוג אחר של מערכת אקולוגית שפועל מול יצורים אחרים לגמרי.
שיווי משקל מקומי קיים גם במערכות אקלים. שינוי עד גודל מסויים יענה במערכות משוב חוזר מחלישות שיחזירו את האקלים למגמה הקודמת שלו, אבל שינוי גדול מידי עלול לגרור תהליכים בלתי הפיכים או מעברי פאזה שיזיזו את המערכת לכיוון של שיווי משקל אחר - לדוגמהחימום של כדור הארץ עקב גורם חיצוני כלשהי עלול לגרור הפשרה של איזורי הקטבים וקרחונים נוספים. קרח הוא לבן ולכן מחזיר כמות גבוהה של הקרינה הפוגעת בו חזרה לחלל. הפשרת קרחונים היא איפה מנגנון שמגביר את התחממות עוד יותר. באופן דומה חימום של האטמוספירה גורר אידוי מוגבר של מי ים, היות ואדים אלה הם גזי חממה חזקים, אידוי של כמות מים גדולה יותר נחשב לגורם שמחזק התחממות בגלל גורם אחר - כלומר סוג של לולאת משוב מחזקת.
השאלה מהו המצב הרצוי של מערכת ביולוגית הוא שאלה נורמטיבית - תלויה בהעדפות המתבונן. עם זאת בדרך כלל החיים מתפתחים כך שיצורים חיים, לרבות האדם, מותאמים לסביבה שלהם עקב תהליך של אבולוציה ביולוגית. מעבר למצב שיווי משקל אחר יכול להתאים למינים אחרים שיתפתחו בהתאמה אליו, אבל הוא עשוי לקחת אלפי או מיליוני שנים, והוא בדרך כלל פחות נוח ליצורים החיים בתקופת השינוי. משום כך שינויים חזקים מידי בסביבה הטבעית עלולים לגרום להכחדה המונית - ובימינו הם באים לידי ביטוי באירוע ההכחדה בהולוקן. אצל בני האדם שינויים כאלה הם באים לידי ביטוי בהתמוטטות ובאופן רחב יותר בבעיות קיימות.
שמירה על שיווי משקל מקומי כתלות בהיסטוריה
הן מערכת אקולוגית והן גוף האדם או גוף של יצור חי אחר הן מערכות בעלות חשל - כלומר היכולת לחזור לשיווי משקל קודם תלויה לא רק בתנאים הנוכחיים או בהפרעה כלשהי בגודל נתון בהווה, אלא גם בהיסטוריה של המערכת ובכמויות של מאגרים שונים שעומדים לרשותה. לדוגמה כריתה של 100 עצים בשנה ביער יכולה להיות בעלת השפעה נמוכה בהתחלה אבל בהמשך לגרום לקריסה אקולוגית של היער.
נדמיין מערכת פשוטה של יער שיש בה רק סוג אחד של עצים. כמות קטנה מידי של עצים לא יצליחו לשמור על חומרי הזנה מספיקים ולכן יתדרדרו, כמות גדולה מידי של עצים תצרוך את כל המשאבים ותגיע לנקודת איזון של יכולת הנשיאה. זו כמובן מערכת פשוטה, ביער אמיתי יש משתנים רבים אחרים המשפיעים על היבט זה, כמו כמות הגשמים, הכמות והתפקדו של בעלי החיים, תנאי מזג האוויר ועוד- וכמובן שאין רק סוג אחד של עצים ביער.
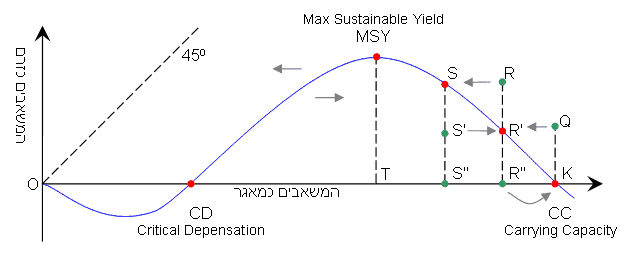
בגרף המצורף, ציר ה-X הוא כמות העצים שכורתים בשנה, ציר ה-Y הוא כמות העצים שיש ביער. העקומה הכחולה מציינת את התנובה בת הקיימא- כריתה של כמות עצים שמאפשרת לשמור על היער בחיים. נקודות ירוקות מסמלות מצבי ביניים - לאחר כריתה של כך וכך עצים בשנה מגיעים לנקודה חדשה על הגרף הכחול (הנקודות האדומות). החיצים השחורים הקטנים מסמלים לאן מוביל אותנו שיווי המשקל החדש. ניתן לראות שכמות העצים שאותה ניתן לכרות השנה, ובכל זאת לשמור על התפקוד על היער תלויה בשאלה כמה עצים יש ביער - כלומר יש לה תכונה של חשל.
הנקודה K מסומנת גם כ-CC מסמלת את יכולת הנשיאה של היער - הוא לא יכיל יותר עצים מעבר לנקודה זו (ללא תשומות מצד בני האדם). בנקודה זו לא כורתים עצים וכמות העצים היא מקסימלית. אם בנקודה K כורתים כמות של Q עצים בשנה, עוברים מנקודה K ומגיעים לנקודה Q וממנה לנקודה 'R שנמצאת על הגרף. בנקודה זו יש התחדשות של Q עצים בשנה, כך שאם לא נכרות עצים מגיעים ל-R תגיים וממנה יש התחדשות ספונטנית של עצים חזרה לנקודה K (שכן היער מתחדש על ידי פינוי נישה לעצים חדשים). אם כורתים בנקודה R רק Q עצים בשנה, נשארים בנקודה R שכן במהלך השנה צומחים עצים חדשים. אבל אם כורתים גודל כפול מזה מגיעים לנקודה חדשה - S - שבה יש פחות עצים וכורתים כמות גדולה יותר בכל שנה. נקודה MSY היא נקודה שבה ניתן להגיע ליבול מקסימלי של עצים באופן מתחדש - כורתים בה T עצים בכל שנה ובכל זאת היער לא קטן. כריתה של פחות עצים בשנה תגדיל את היער ותאפשר לכרות יותר עצים בשנה הבאה, כריתה של יותר עצים תקטין את גודלו של היער תאפשר לכרות פחות עצים בשנה הבאה. בנקודה CD כריתה של עץ אחד תוביל להתדרדרות ספונטנית של היער. מתחת לנקודה זו יש לנטוע בכל שנה כך וכך עצים רק כדי שהיער יישאר בגודל יציב. ראו הסבר נוסף בדיילי: כלכלה אקולוגית, פרק 6, משאבים ביוטיים.
אפשר לראות בגרף גם את האיזורים יש יציבות או אי יציבות של נקודות שיווי משקל. הן נקודה CC והן נקודה CD והנקודה 0 הן נקודות של שיווי משקל שבהן לא כורתים עצים וכמות העצים ביער נשארת זהה. נקודות CC ו-0 הן נקודות שיווי משקל יציבות - שינוי קטן וחד פעמי יחזיר אותנו עליהן, נקודה CD היא לא יציבה - הפרעה קטנה וחד פעמית תדחוף את היער בכיוון CC או O. בין הנקודה CC לנקודה MSY יש איזור של שיווי משקל יציבים מקומית. סטייה קטנה מעל או מתחת לכמות העצים באיזור זה גוררת חזרה אל הגרף הכחול. בין הנקודות MSY לנקודה CD יש איזור של נקודות שיווי משקל לא יציבות - סטייה קטנה מתחת לגרף הכחול (כריתה של פחות עצים בשנה ביחס לכמות בת קיימא) מובילה לנקודת MSY. סטיה מעל לגרף הכחול מובילה באופן ספונטני לנקודה CD שבה היער יכול להתקיים אבל ללא כריתה. נקודה CD עצמה אינה שיווי משקל יציב, נטיעה של עוד עץ אחד תוביל לנקודה MSY, כריתה של עץ אחד מובילה להתדרדרות ספונטנית עד לכמות של 0 עצים.
השקפות שונות על שיווי משקל בהקשר של אקלים ומערכות ביולוגיות
לעיתים תכופות אנשים מתקשים לקלוט את ההתנהגות של מערכות מורכבות ולכן מייחסים למערכת תכונות פשוטות יותר - כלומר מייחסים למערכת קיום של שיווי משקל יציב (ומתפקד) או מייחסים לה שיווי משקל בלתי יציב.
לדוגמה השערת גאיה מניחה כי בכל מקרה הביוספרה תדע להתאים את עצמה ולהימנע מקריסה - כלומר שיווי משקל בודד ויציב. השערה נגדית שיש אנשי סביבה שמחזיקים בה היא מצב הפוך - שבו שיווי משקל בלתי יציב, וכל שינוי קטן בסביבה יגרום לקריסה. לעומת שתי תאוריות אלה, השערת מדיאה מניחה קיום של מספר מצבי שיווי משקל שחלקם יציבים ואחרים פחות, כאשר מדי פעם המערכת מגיעה לחוסר יציבות וגולשת לכיוון של שיווי משקל אחר - כאשר תוצאה אפשרית של מעבר כזה היא הכחדה המונית, השערת מדיאה מדגישה גם ששינוי כזה לא חייב להיות פתאומי והוא יכול להתרחש על פני תקופת זמן ארוכה - כלומר ייתכן מצב של שינוי קטן ובלתי מורגש כמעט המתמשך על פני זמן ממושך ומושך אותנו לכיוון של שיווי משקל אחר.
מומחה הסיכונים John Adams טען בשנת 1995 כי לאנשים יש תפיסה שונה לגבי הטבע, חלקם מניחים כי הוא מערכת יציבה וכי לא משנה מה האדם יעשה הטבע הוא נדיב ויציב ויתמודד עם זה בלי פגיעה ברווחה שלנו. לעומת זאת יש אנשים שחושבים שהטבע הוא הפכפך וכי הפרעה קטנה מאוד של האדם תגרום לקריסה כוללת. השקפה שלישית היא כי יש מספר רב של שיווי משקל וכי שינוי גדול מידי ידחוף לכיוון של שיווי משקל חדש (אם כי שיווי משקל זה יכול גם לכלול הכחדה של האדם) נקודת השקפה רביעית מניחה כי יש שיווי משקל אדיש וכי לאדם אין השפעה מהותית על שיווי המשקל שהטבע יהיה בו[2], חוקר האקלים, פרופסור Mark Maslin, טען כי דפוסים אלה מאפיינים גישות שונות ביחס לנושא התחממות עולמית ושינויי אקלים. מכחישי אקלים ואנשים רבים בימין מאמינים שהאקלים הוא יציב ושהאדם לא יכול לשנות אותו (שיווי משקל יציב) ואילו ארגוני סביבה כמו גרינפיס מדגישים יתר על המידה את הסיכונים בגלישה לחוסר יציבות, הוא מעריך כי רוב המדענים מאמינים באפשרות השלישית של ריבוי שיווי משקל מקומיים. [3]
שיווי משקל בכלכלה
 ערך מורחב – ריבוי שיוויי משקל בכלכלה
ערך מורחב – ריבוי שיוויי משקל בכלכלה
אחת ההנחות הפופולריות בכלכלה נאו-קלאסית הוא הקיום של שיווי משקל יציב ויחיד - הן כשיווי משקל בין קונים למוכרים ביחס למכירים והכמויות בשוק מסויים (שיווי משקל חלקי) והן ביחס לשיווי משקל בכלל השווקים - שיווי משקל כללי. כלכלנים הטרודוקסיים כמו סטיב קין וכלכלנים מזרם של כלכלה אקולוגית חולקים על הנחות אלה ומניחים כי בשוק ייתכנו מספר שיווי משקל מקומיים בעלי יציבות מקומית.
שיווי משקל וחופש
בהגות הליברלית קיימת הנחה לא פורמלית לגבי יציבות של מערכות. הליברלים טוען כי לאנשים יש זכויות כמו זכויות אדם וזכויות אזרח, כל עוד זכויות אלה לא מפריעות לאנשים אחרים - אין סיבה מוסרית למנוע מאנשים את החופש שלהם. הליברליזם ממשיך ומתאר שורה זכויות שיש אותם לאנשים כמו הזכות לחיים, הזכות לקניין, חופש הביטוי, חופש התנועה וכו'.
אחת הבעיות בהגות הליברלית היא קושי להבחין במערכות פיזיקליות, ביולוגיות, חברתיות או כלכליות שיכולות להגביל את צורות החופש האלה, וכן בתנאים, חוקים, טכנולוגיות ומצבים כלכלים שעלולים לגרום לשינוי במערכות האלה בצורה שתגביל את החופש של האנשים או שתאיים על הקיום של כלל האנשים במערכת חברתית נתונה.
דוגמה לכך היא שמירה על שיווי משקל בספינה כדי שזו לא תטבע. כאשר יש משקל רב מידי סביב אחד הצירים שלה, הספינה עלולה להתהפך. ספינה צפה על ידי דחייה של מים על ידי אוויר, והתהפכות כזו מכניסה מים לתוך הספינה, ולכן התהפכות כזו עלולה לגרום לספניה לטבוע. בספינה גדולה אין כל בעיה שאנשים ילכו לכל מקום באוניה. הספינה גדולה וגם אם כל הנוסעים בספינה ילכו לירכתיים הדבר ישנה את זווית הספינה רק בכמה מאיות-מעלות בודדות. לעומת זאת ככל שהספינה קטנה יותר (סירה) או שיש יותר נוסעים בספינה או שכל נוסע הוא גדול יותר - כך יש קושי לשמור על חופש התנועה בתוך הספינה. מגבלה שכלל אינה קיימת בספינה גדולה הופכת להיות מגבלה סטטיסטית בספינה קטנה יותר (אפשר להסתובב בחופשיות אבל יש צורך לשמור שאנשים שונים לא יהיו באותו מקום באותו זמן) ובסירה או דוברה חופש התנועה מוגבל עור הרבה יותר. כמובן שגם גודל הנוסעים חשוב - אם בספינה שלנו הנוסעים הם פילים במקום אנשים - אז חופש התנועה שלה יורד ככר בנפח ספינה נמוך יותר. באופן דומה - אם יש הרבה אנשים (גידול אוכלוסין) המשקל הכולל של כולם עלול לגרום בעיית שיווי משקל במקרים מסויימים - גם בספינות גדולות.
ביחס לשיווי משקל מכאני יש גם היבט נוסף - המספר הגדול יותר של אנשים בספינה פירושו בדרך כלל פיזור של משקל הנוסעים בכל רחבי הספינה בהסתברות גדולה יותר. אם לדוגמה היו רק 2 נוסעים בספינה הסיכוי ששניהם נמצאים באותו מקום בספינה הוא גדול יותר. היבט זה נכון לחלק מסוגי שיווי המשקל כאשר אנשים שונים יכולים לאזן זה את זה - כמו בשיווי משקל מכאני, היא פחות נכונה כאשר כלל האנשים מפעילים יחד כוח משותף מול מערכות אקולוגיות - לדוגמה פליטה של פחמן דו חמצני או צריכה של אנרגיה מייצור ראשוני.
אפשר להכליל את הנושא של שיווי משקל לנושאים אחרים - לדוגמה ביחס להגנה ממגיפות, להגנה משריפות, הצורך להגן על מערכות אקולוגיות, יציבות חברתית ועוד. גורמים שונים במערכת החברתית - כמו יותר אנשים, יותר כוח כלכלי ויותר כוח טכנולוגי או מדעי (ידע הוא כוח) יכולים להשפיע על מידת החופש שיש לאנשים בגלל שהם עלולים לצמצם את התחום שבו פעולות שונות לא משפיעות על יציבות המערכת. לדוגמה יכולת נסיעה מהירה יותר בכלי רכב - אופניים, מכוניות, מטוסים, חלליות - פרושה צורך בהפעלת כוח פיזי רב יותר (לשם תאוצה מהירה יותר) וכן כוח פיזי ופוליטי רבים יותר - שכן רמת האיום של כלי התחבורה הם גדולים יותר. הכוח הרב יותר של הפרט מגדיל את האיום של פרט כזה על חייהם של אנשים אחרים. אם רוצים למנוע סיכון מאנשים אחרים, דבר זה מחייב הפעלת רגולציה גדולה יותר או חיוב שימוש בטכנולוגיה שתשמור על אנשים אחרים. באופן דומה גם מרחב צפוף יותר - עם יותר אנשים - דורש יותר מגבלות, משום שהסיכוי להתנגשות חמורה הוא גדול יותר במרחב צפוף יותר.
ספינת החלל כדור הארץ
דבר זה בא לידי ביטוי בחלק מהדיונים על ספינת החלל כדור הארץ והשוואה שלה לבוקרים במערב הפרוע. במערב הפרוע הצפיפות נמוכה, ההשפעות ההדדיות הן נמוכות, וחופש פעולה של אדם אחד כמעט ולא משפיע על אנשים אחרים. בקצה השני של הסקאלה, בספינת חלל, פעולות כאלה עלולות להיות קטלניות לחלק גדול מהאנשים או להוות איום קיומי לכלל החברה.
לדוגמה ירי באוויר ברובה הוא לא מסוכן במיוחד במערב הפרוע. בעיר צפופה דבר זה יכול לסכן אנשים בסיכון נמוך בגלל הקליע שיורד בחזרה. בספינת חלל או התיישבות בחלל ירי בודד כזה עלול להרוג את כולם. מגבלות דומות קיימות לגבי שריפה זיהום או מגבלות משאבים (של משאבים מתכלים או שיבוש של מחזור ביו-גאו-כימי של יסודות שחיוניים לקיום כלל הנוסעים כמו מחזור הפחמן, מחזור הזרחן וכו'.
דבר זה בא לידי ביטוי בניסוי ביוספרה 2 כאשר יש מערכת אקולוגית ענקית כמו כדור הארץ היא יכולה לתמוך בחיים כמה מיליארדים של אנשים. בניסוי "ביוספרה 2" ניסו לקיים מערכת אקולוגית קטנה יותר שניסה לתמוך בחיים 8 אנשים שדימו התיישבות בחלל (נניח מושבה על הירח או מאדים). ניסוי ביוספרה-2 נכשל כאשר המערכת יצאה מאיזון. יותר קל לצאת מאיזון ככל שההשפעה האנושית היא גדולה יותר ביחס למערכת האקולוגית וככל שיש בזו פחות מינים ומנגוניים של איזון חוזר שיכולים לדאוג לחוסן של מערכות אקולוגיות (שיבה לשיווי משקל לאחר סטיה קטנה ממנו). אם כתוצאה מטביעת רגל אישית גבוה יותר בממוצע או בעקבות זה שיש אוכלסייה אנושית גדולה יותר.
דבר זה נכון גם ביחס לשאלות של ילודה. בחברה עם צפיפות נמוכה השפעות של ילודה גבוה הן נמוכות, בחברה עם צפיפות גבוה יותר השפעות הילודה הן גבוהות יותר בגלל קרבה גדולה יותר של המערכת לתנאי סף שלה. בספינה במשקל של 200 טון אין השפעה לכמות הילדים שילדו שתי אמהות, אבל אם משקל הנוסעים עצמו מתקרב כבר ל-200 טון (נניח כ-4,000 נוסעים) אז הולדה של עוד ועוד ילדים פרושה סיכון כלל חיי הנוסעים (אנו מניחים כמובן שמזון שמגיע מחוץ לספינה תורם להגדלת המאסה הכוללת של הנוסעים - בדומה לכך שהמערכת האקולוגית מאפשרת גידול של המאסה של כלל האנושות). חופש שהוא מובן מאליו בחברות לא צפופות - החופש להוליד ילדים, הופך להיות לא מובן מאליו בחברה צפופה.
ראו גם
- השערת גאיה, השערת מדיאה
- מערכות מורכבות
- לולאת משוב
- חשל, עמידות, רובסטיות
- שיווי משקל סטטי
- מערכת דיאספטית
קישורים חיצוניים
- סוגים של שיווי משקל בוויקיפדיה האנגלית
- שיווי משקל מכאני בוויקיפדיה האנגלית
- שיווי משקל תרמודינמי בוויקיפדיה האנגלית
- הומאוסטאזיס בוויקיפדיה האנגלית
- שיווי משקל מקוטע באבולוציה בוויקיפדיה האנגלית
- ריבוי נקודות שיווי משקל בוויקיפדיה האנגלית
| מערכות מורכבות |
|
מושגי יסוד: הוליזם - שיווי משקל - תהליך - אנטרופיה - אקסרגיה - החוק השני של התרמודינמיקה - מידע - ארגון עצמי - הגחה - לולאת משוב - תהליך בלתי הפיך - עמידות - חשל - גידול מעריכי - תגובת יתר |
|
מערכות, מודלים וגישות: מערכת מורכבת - מערכת מפזרת - מודל מבוסס סוכנים - מערכת מורכבת אדפטיבית - חשיבה מערכתית - דינמיקה של מערכות - תורת המידע - כלכלה אבולוציונית - כלכלת מורכבות - שיטת המערכות הרכות |
|
מערכות ואקולוגיה: תהליך ארוך טווח - מחזור ביוגאוכימי - חוק המינימום של ליביג - פרדוקס ג'בונס - עקרון ההספק המקסימלי - הולון - אנרגיה גלומה - שירותי המערכת האקולוגית - ייצור ראשוני - מטבוליזם |
|
ספרים ומאמרים: ספינת החלל כדור הארץ - גבולות לצמיחה - מעבר לגבולות - חוק האנטרופיה והתהליך הכלכלי - תריסר נקודות מינוף להתערבות במערכת - דינמיקת מערכות פוגשת את העיתונות - עיצוב כלכלה הוליסטית לעולם בר קיימא |
|
אישים, הוגים וארגונים: דונאלה מדווז - ניקולס ג'ורג'סקיו-רוגן - האווארד ת. אודום - דיוויד בוהם - איליה פריגוז'ין - מכון סנטה פה |