מערכת מורכבת

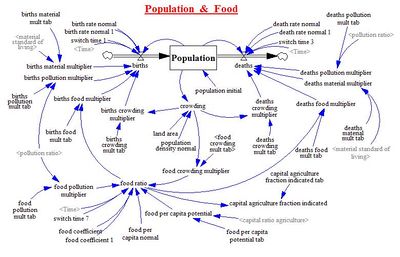
תיאור גרפי של חלק ממודל עולם 3, מתוך הספר גבולות לצמיחה. התמונה מתארת זרמים ומאגרים, קשרי גומלין ולולאות משוב. מודל עולם 3 מדגים חשיבה הוליסטית שנובעת מתוך דינמיקת מערכות שהיא סוג של ניתוח של מערכות מורכבות.

מערכת מורכבת (באנגלית: Complex system) היא מערכת הבנויה מחלקים שונים המקיימים ביניהם אינטראקציה לא-לינארית ואשר כיחידה אחת יש להם תכונות שאינן ברורות מאליהן מתוך התכונות של הרכיבים הבודדים (הגחה).

דוגמאות למערכות מורכבות כוללות: מערכות פיזיקליות (כמו זרימה של נוזלים וגזים ומערכות תרמודינמיות), צבירי כוכבים, מערכת האקלים של כדור הארץ, תאים ביולוגיים, מערכות עצבים, מושבות חיידקים, יצורים חיים, מושבות נמלים, מערכות אקולוגיות, הביוספרה, מפעלים כימיים גדולים, אוניות, נמלי תעופה, תשתיות תקשורת ואנרגיה, ערים, רשתות תחבורה, בני אדם כיצורים ביולוגיים ופסיכולוגיים, כלכלות, חברות אנושיות ועוד.

מערכות מורכבות נחקרות כיום במסגרות אליהן שייכות המערכות המדוברות בכל תחומי המחקר המדעי - במדעי הטבע, במתמטיקה ובמדעי החברה. שדות שמתמחים במחקר הבין-תחומי של חקר מערכות מורכבות כוללים את תורת המערכות (או מדעי המערכות), תורת המורכבות, אקולוגיה מערכתית וקיברנטיקה. תחומים ליישום כוללים ביולוגיה, רפואה, רפואה מונעת, תכנון ערים, אקולוגיה, כלכלה התנהגותית, כלכלה אקולוגית, תכנון ארוך טווח בתחומי צבא ותשתיות ועוד.

מעבר לעובדה שמערכות מורכבות רבות הן רשתות מסוגים שונים, ושהם מורכבים, נדמה לפעמים שאין ביניהם הרבה מן המשותף, ולכן המושג "מערכת מורכבת" יכול להראות כריק מתוכן. אולם, למערכות מורכבות יש מאפיינים התנהגותיים ומבניים משותפים, שמאחדים את כולן כתופעות. הדברים דומים גם מבחינה תאורטית, מכיוון שאפשר לייצג את כל המערכות האלו באופן מוצלח (פחות או יותר) על ידי סוג מסוים של מתמטיקה, ולכן אפשרי לקבוע באופן מדוייק ופורמלי יחסית את המאפיינים המשותפים לכל המערכות האלו או לתתי קבוצות של מערכות.

הגדרה פורמלית

באופן פורמלי, המושג מערכת מורכבת מתייחס למערכת בעלת חלקים רבים שמחוברים ביניהם באופן לא לינארי. מערכת כזו עשוייה להיות דיסקרטית (בדידה) או רציפה. מכיוון שהן לא-לינאריות, מערכות מורכבות הן יותר מהסך של כל חלקיהן, מכיוון שמערכת לינארית עונה לעיקרון של סופרפוזיציה, ולכן היא הסך של כל חלקיה, ואילו מערכות לא-לינאריות אינן כאלה. כלומר: יחס לינארי הוא כזה שהגרף שלו הוא קו ישר, כך שהשינוי בגורם אחד מביא לשינוי פרופורציונלי באחר. חיבור לא-לינארי פירושו ששינוי בצד אחד אינו פרופורציונלי לשינוי באחר. כאשר יש מרכיבים לא-לינאריים רבים במערכת, ההתנהגות שלה עשויה להיות בלתי ניתנת לחיזוי. מדע המערכות המורכבות חוקר התנהגות כזו.

שני סוגים נוספים של אי-לינאריות הם:

לולאות משוב: מערכת בה הפלט חוזר כקלט (Feedback) תציג התנהגות מורכבת - מחד ניתן לשמור על מצב שיווי משקל, מאידך אפשר לקבל התבדרות מהירה, כאשר ההבדל בין שני המצבים יכול להיות שינוי קטן באחד הגורמים במערכת.
זיכרון: מערכת בעלת זיכרון אינה ניתנת לניתוח בכלים לינאריים והיא יכולה להציג התנהגויות שונות כאשר חוזרים על סיטואציה מסוימת שוב ושוב ('למידה').

רוב המערכות הביולוגיות הן מערכות מורכבות במשמעויות הללו, ואילו רוב המערכות הבנויות בידי אדם אינן כאלה. מדע המערכות המורכבות חופף עם מחקר הדינמיקה הלא-לינארית, אך מערכות מורכבות כוללות מספר גדול של חלקים דינמיים שפועלים בתוכן.

התפתחות המחשב אפשרה לחקור את נושא המערכות המורכבות ונתנה דחיפה עצומה לחקר התחום כולו. חוקרים מתחומי מחקר רבים מתעניינים בענף זה של מחקר מתמטי ומחקרם מתפתח בד בבד עם שכלול הטכנולוגיה המאפשרת אותו.

הגדרה לא פורמלית של מערכות מורכבות

הוצעו תיאורים לא פורמליים שונים של מערכות מורכבות. מהדורה מיוחדת של כתב העת Nature על מערכות מורכבות (כרך 284, מספר 5411 (1999)) הציגה כמה מהם:

מערכת מובנית מאוד, בעלת מבנה עם ווריאציות.
כזו שההתפתחות שלה רגישה מאוד לתנאים הראשוניים או לשינויים קטנים, או כזו שיש לה אפשרויות רבות מאוד להתפתחות.
כזו שמספר הרכיבים הפועלים זה על זה הם רבים.
כזו שבשל עיצובה או הפעולות שלה, או שניהם, קשה להבין או לבדוק אותה.
מערכת שנמצאת בעיצומו של תהליך, שגורם לה להשתנות ולהתפתח במשך הזמן.

התנהגות של מערכות מורכבות

מערכות מורכבות עשויות, מעצם הגדרתן, להציג התנהגות מורכבת ומאוד לא-סדירה, שבה קשה לחזות מה שינוי במרכיב מסוים יעשה במשך הזמן. אולם, מערכות מורכבות עשויות גם להציג התנהגות פשוטה יחסית, בדומה למערכות לינאריות. אמנם, שלא כמו מערכות לינאריות (גם המסובכות ביותר), מערכות מורכבות לא-לינאריות גמישות מאוד בהצגת התנהגות שונה מבחינה איכותית בזמנים שונים. במערכות מורכבות, שינוי כזה ידוע כביפורקציה. חלק מהמחקר במערכות מורכבות עוסק בנסיון להתחקות אחר חוקים שמתארים את ההתנהגות של הפשוטה של מערכות מורכבות.

יישומים של תאוריית המערכות המורכבות

מחקר המערכות המורכבות מפיח חיים חדשים בתחומים רבים של המדע, שהאסטרטגיה הרדוקציוניסטית לא הצליחה להסביר אותם. לפיכך, מדע זה עוזר לפתור בעיות רבות בתחומים שונים כמו נוירולוגיה, מטאורולוגיה, פיזיקה, מדעי המחשב, חיים ‎מלאכותיים, מיחשוב אבולוציוני, כלכלה, חיזוי רעידות אדמה, תאום של תאי לב, מערכות חיסוניות, אפילפסיה ועוד. במחקרים אלה, המדענים מנסים בדרך כלל להבין את החוקים הלא-לינאריים הפשוטים שגורמים לתופעות המורכבות (ולא לתאר את התופעות האלה). חברות אנוש (וכנראה גם מוחות בני האדם) הם מערכות מורכבות שגם המרכיבים שלהן וגם הקשרים ביניהם אינם פשוטים. אף על פי כן, יש להן את התכונות של מערכת מורכבת.

באופן מסורתי, ההנדסה ניסתה לשמור על הלינאריות של המערכות שלה, מכיוון שכך קל יותר לבנות אותן ולחזות את התנהגותן. אולם, מערכות פיזיקליות רבות (לדוגמה לייזרים) הן מערכות מורכבות על פי ההגדרה שהצגנו, ולכן על ההנדסה לכלול גם מרכיבים של מחקר המערכות המורכבות.

היסטוריה של התחום

החל משנות ה-70 חוקרים החלו להבין שהבעיות המורכבות שעומדות בפניהם בתחום המחקר שלהם, הינן בעלות מאפיינים משותפים לבעיות מתחומים אחרים, שלכאורה אין קשר אליהם. בתהליך ארוך של תקשורת בין תחומי מחקר שונים, והתגברות על בעיות אגו, הבינו חלק מהחוקרים שהם בעצם חוקרים את אותו תחום שנקרא מערכות מורכבות, או סיבוכיות (Complexity), קצת כמו העיוורים הממששים פיל, כל אחד מהם ראה בעבר חלק אחר שמאפיין התנהגות של מערכות מורכבות.

כמו נושאים רבים, הפופולריות של הנושא יודעת גלים של עליות וירידות. למרות שג'י פורסטר לדוגמה פיתח את התחום כבר בשנות ה-70, הוא לא זכה לתהודה רבה, אולי בגלל השימוש הרב במחשבים או בגלל שהאליטות הישנות באקדמיה חששו למעמדן. מכל מקום התחום היום הוא "בוגר" - הוא מספק תוצאות בשטחי מחקר שונים, וספרים חדשים נכתבים בנושא, והפופולריות שלו בתחומי מחקר שונים, כולל בכלכלה, עולה כל הזמן.

ועם זאת, המטרות של חוקרי המערכות המורכבות הפכו להיות צנועות יותר. אם בעבר חלק מהם חלמו על מהפכות מדעיות עבור כל המערכות המורכבות, כיום מתרכזים בקבוצת החוקים ששולטת בדינמיקה של קבוצות של מערכות ספציפיות ורק לאחר מכן בחוקים בסיסיים המשותפים לכל הקבוצות.

כמו כן, כענף צעיר, סיבוכיות צריכה לפתור בעיות רבות כמו קונצנזוס על טרמינולוגיה, הגדרות בסיסיות, אמות מידה, ומיון הידע. כמו כן יש צורך לשפר את המבנים התאורטיים ולבצע עוד הרבה בדיקות אמפיריות.

דוגמה לשאלות פתוחות - מה זה בדיוק "סיבוכיות" או "מערכות מורכבות"? מהי "הגחה" ואיך היא "מגיחה"? איך ממדלים ומסבירים את הדינמיקה שמערכות מסוגלות לקיים? (כמו "התנהגות תלויית מסלול" או "קפיצה בענפים בעץ האפשרויות", "נעילות" ומולטי-מודל".

מאפיינים של מערכות מורכבות טבעיות

היחסים בתוך המערכת הם לא תמיד לינאריים

גידול מעריכי (קו ירוק) גדל בקצב גדול יותר מאשר פונקציה לינארית (קו אדום) או ריבועית (קו כחול).

ערך מורחב – אי-לינאריות

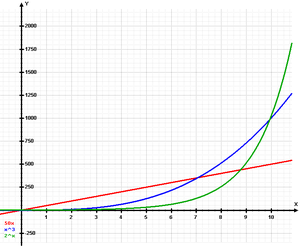
במערכות לינאריות, ההשפעה הינה פרופורציונלית לשינוי. אם מגדילים את המהירות נגיע פי שתיים יותר מהר. במערכות לא לינאריות המצב מסובך יותר והתגובה יכולה להשתנות. במונחים מעשיים, משמעות הדבר היא ששינוי קטן של גורם אחד במערכת יכולה שלא לעורר כל תגובה, לעורר תגובה פרופורציונלית לשינוי או לגרום לשינוי גדול (אפקט הפרפר), להשפעה דומה בגודלה, או להיות חסרת השפעה. ייתכן גם כי פעולה היא חסרת השפעה לכאורה לזמן נתון אבל היא גורמת לשינוי נסתר שמתפרץ מאוחר יותר בצורה פתאומיות יותר.

ארגון עצמי

ערך מורחב – ארגון עצמי

"רובה הגלשנים" מדגים ארגון עצמי במסגרת מדעי המחשב- תאים בעלי חוקים פשוטים מאוד יוצרים באופן ספונטני דפוסים של סדר, אבל באופן שקשה לחזותם מראש.

מרגע שהגיעו למסה קריטית של משתתפים או רכיבים, הם מתארגנים באופן ספונטני כדי ליצור מערכת דינמית בעלת היררכיות עוקבות. דבר זה מתבצע באמצעות השפעה או התאמה הדדית ללא הכוונה, תכנון או תכנות מרכזי. דבר זה מכונה ארגון עצמי

עם מעט אינטליגנציה (ולפעמים אפס אינטליגנציה), מידע מקומי וחוקים פשוטים לאינטראקציה חלקי המערכת יכולים ליצור התנהגות מערכתית מסובכת מאוד, דבר זה נובע בחלקו מלולאות משוב מחזקות אשר עשוית להתרחש מאירועים במהלך ההיסטוריה של המערכת. אירועים אלה מתקיימים (לפחות כסיבה חלקית) עקב יתרונות לגודל, כמו אלו שיכולים להתרחש עקב אפקט רשת. עקב כך אין צורך בהנחות חזקות על היכולות, הידע או הרציונליות של המשתתפים, (אם כי תכונות אלו אינן אסורות).

דוגמאות בולטות ל"מסה קריטית" המייצרת התנהגות מורכבת הינן תהליך הגחת החיים (המכונות המשכפלות ב"גן האנוכי") - הצטברות של מולקולות שונות בתנאים מסויימים הובילה ליצירת מכנות משכפלות יותר ויותר מורכבות ולבסוף ליצירה של תאים ויצורים שלמים. דוגמאות נוספות כוללות מוח המורכב מתאים בעלי התנהגות חיצונית פשוטה יחסית, מסיבה, או סופת הוריקן המורכבת ממים במצבי צבירה שונים ומאנרגיה, וכן מודלים "אבולוציוניים" של סוכנים מתורת המשחקים.

הגחה

ערך מורחב – הגחה

מרגע שנוצרה, מערכת מרוכבת מייצרת תכונות מפתיעות, הנקראות "תכונות מגיחות", שלא ניתן לחזות אותן מראש מתכונות של המרכיבים או המשתתפים, מהחוקים של האינטראקציה או מקומבינציה כלשהי של חוקים ותכונות של משתתפים בודדים או אפילו "מעטים מידי".

"היד הנעלמה" של אדם סמית הינה דוגמה קדומה להגחה - לא המוכרים ולא הקונים חושבים על המנגנון של ויסות המחירים על ידי שוק, ובכל זאת במספר רב של קונים ומוכרים אפשר להגיע לתבנית של יציבות יחסית של מחירים וכמויות. דוגמה נוספת היא מוזיקה - אשר נובעת לא מהצלילים עצמם אלא מהיחסים בין הצלילים.

אי שיווי משקל

ערכים מורחבים – שיווי משקל, הפרפר של לורנץ

יש מערכות מורכבת בהן סביר שהמערכת תתקיים יותר זמן באי-שיווי משקל מאשר בשיווי משקל, ואין שום הבטחה שיציאה משיווי משקל תהיה למשך זמן קצר או ל"מרחק" קצר (כלומר שהשיווי משקל יהיה יציב). רעיון זה בוטא בזמנו בכלכלה על ידי ג'ון מיינרד קיינס ("בטווח הארוך נהיה כולנו מתים"), והוא מתאים להתנהגות של מערכת תרמודינמית - שהיא מעניינת (או מבצעת עבודה) כל עוד היא נמצאת מחוץ לשיווי משקל.

המצאות בשיווי משקל פירושה במקרים רבים קיום של אי יעילות ושמתחרה עלול לדרוס אותך כליל (תחרות שומפטריאנית לדוגמה) - לדוגמה תאגידי הרכב בארצות הברית לפני הכניסה של תאגידי המכוניות היפניים, או שיווי משקל של מינים באי לפני כניסה של מינים פולשים מהיבשת. כמו כן פעמים רבות למערכת יש כמה שיווי משקל או שהיא נעה סביב כמה מהם.

קשרים מכילים לולאות משוב

ערך מורחב – לולאת משוב

דוגמה ללולאת משוב מחזקת: שריפה ביער- עד גבול מסויים ככל שהשריפה חזקה יותר כך היא מתחזקת עוד יותר. במערכות מורכבות אמיתיות אין לולאת משוב אחת, אלא אוסף של לולאות משוב מחזקות ומחלישות.

במערכות מורכבות ניתן למצוא בדרך כלל לולאות משוב, הן מחלישות והן מחזקות. ההשפעות של התנהגות אלמנט בודד מוזנות אליו בחזרה באופן כזה כך שהוא עצמו משתנה.

מערכות תרמודינמיות פתוחות

ערך מורחב – מבנה מפזר

מערכות מורכבות הן בדרך כלל מערכות תרמודינמיות פתוחות - דרך גבולות המערכת זורם כל הזמן שטף של אנרגיה ושל חומר. כלומר, מערכות מורכבות כאלה הן רחוקות משיווי משקל אנרגטי, ומכלות אקסרגיה באופן תמידי. אבל למרות השטף הזה, הן בעלות דפוס התנהגות יציב. ראו סינרגטיות

למערכות מורכבות יש היסטוריה

ערכים מורחבים – חשל, תהליך בלתי הפיך

ההיסטוריה של מערכות מורכבות יכולה להיות חשובה. בגלל שמערכות מורכבות הינן מערכות דינמיות, הן משתנות במשך הזמן, והמצבים הקודמים עשויים להיות בעלי השפעה על המצב הנוכחי. באופן פורמלי יותר, מערכות מורכבות יכולות לחוות חשל. הכוונה היא שאם מסתכלים על התנאים או על הקלט שבהם המערכת נמצאת כרגע, לא בהכרח אפשר להבין איך המערכת תתנהג.

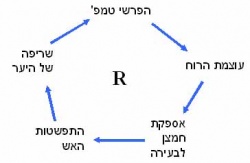
במערכת פשוטה, לדוגמה כדור הנמצא במישור משופע, או חימום של מים, אפשר לדעת איך המערכת תתנהג לפי המצב הנוכחי, ההיסטוריה אינה חשובה. לעומת זאת במערכות מורכבות אם נבצע אותן פעולות על המערכת היא יכולה להתנהג בצורות שונות כתלות בהיסטוריה שלה. לדוגמה אם נכרות כמות מסויימת של עצים ביער בכל שנה הוא יכול להשתקם או לא להשתקם כתלות בהיסטוריה שלו.

הכלה של מערכות אחרות

הרכיבים של מערכת מורכבת יכולים להיות בעצמם מערכת מורכבת. לדוגמה, כלכלה מורכבת מארגונים, המורכבים מאנשים, המורכבים מתאים - וכל אלה הן מערכות מורכבות.

קושי לקבוע את מיקום הגבולות

יש מערכות מורכבות רבות בהן קשה לקבוע מה המיקום הנכון של הגבול או המעטפת של מערכת מורכבת. במקרים אלה ההחלטה מתקבלת בסופו של דבר על ידי החוקר או על ידי המחקר שבמסגרתו נחקרת המערכת. דוגמה לכך היא המחקרים מהשנים האחרונות החוקרים את המיקרוביוטה - אוכלוסיית החיידקים החיה על בני האדם ובתוכם, נמצאת באינטראקציה עם התאים של הגוף האנושי ומשפיעה על תהליכים שונים כמו עיכול או תגובות של המערכת החיסונית.

רשת דינמית ומגוון

הדינמיות של רשת החיבורים המשמשת את המערכת המורכבת גם היא חשובה. במערכות מורכבות רבות יש רשתות בעלות חיבורים מקומיים רבים ומעט חיבורים בין-אזוריים. לדוגמה, בקורטקס של המוח האנושי אנו רואים הרבה איזורים של חיבוריות מקומית רבה, ומעט אקסונים ארוכים המחברים בין אזורים בתוך הקורטקס לבין אזורים אחרים. זה דוגמה לכך שמערכות מורכבות הן לרוב לא הומוגניות אלה מכילות מגוון של תצורות ורכיבים שונים זה מזה הפועלים יחד.

ראו גם

קישורים חיצוניים

מערכת מורכבת בוויקיפדיה האנגלית
כלכלת סיבוכיות ואלן גרינספן, מדוע מערכות מורכבות חשובות בכלכלה והכניסה שלהם למיינסטרים, Lewis L. Smith, כלכלה פוסט אוטיסטית.