פונקציית ייצור קוב-דאגלס
בחקר הכלכלה פונקציית ייצור קוב-דאגלס (באנגלית: Cobb–Douglas production function) היא משוואת ייצור פופולרית במסגרת מודלים במיקרו-כלכלה ובמאקרו-כלכלה נאו-קלאסית המשמשת להדגמת היחסים שקיימים לכאורה בין כמויות של שני גורמי ייצור או יותר לבין הכמות הכוללת של מוצרים או שירותים שנוצרים במפעל או בפירמה בתקופה נתונה. השימוש הנפוץ בפונקציה הוא להדגמת גורמי ייצור של הון תעשייתי ועבודה. לפעמים משתמשים במושג בצורה מגבילה יותר, כך שנדרשת תשואה קבועה לגודל.
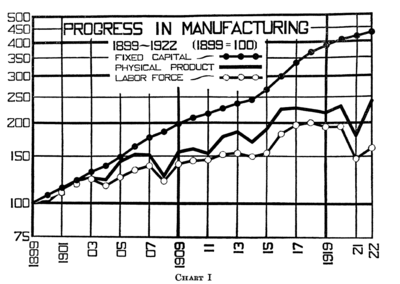
משוואת קוב-דאגלס פותחה ונבחנה מול מידע סטטיסטי הנוגע לתעשייה בארצות הברית על ידי הכלכלן Paul Douglas והמתמטיקאי Charles Cobb ראשית על מידע שנאסף בשנים 1899-1922.[1]לאחר מכן על מידע נוסף שנאסף בשנים 1927-1947. הפונקציה אמורה לייצג התנהגות מיקרו-כלכלית של מפעל או של שוק, והיא משמשת לעיתים קרובות גם במאקרו-כלכלה. למרות השימוש הרב שנעשה בה, קיימת מחלוקת ארוכת שנים לגבי ההגיון שיש בפונקציה והשימוש בה בתחומי המיקרו-כלכלה והמאקרו-כלכלה.
ניסוח פורמלי
בניסוח הסטנדרטי ביותר של ייצור מוצר בודד עם שני גורמים ייצור הפונקציה היא
- Y=ALαKβ
כאשר:
- y = היא כמות הייצור הכוללת (הערך ה"ריאלי" של כל המוצרים שנוצרו בתקופה מסויימת, לדוגמה בשנה)
- L = כמות תשומות של עבודה (כמות שעות העבודה של כלל העובדים במפעל בשנה אחת)
- K = כמות תשומות של הון תעשייתי (שנמדד בצורה על ערך ריאלי של כל המכונות, הציוד והמבנים המעורבים בתהליך הייצור)
- A גורם פרודוקטיביות כללי.
- α ו-β נקראים גורמי גמישות התפוקה (Output elasticity) של העבודה ושל ההון בהתאמה. גורמים אלה אמורים להיות קבועים בהינתן סוג מסויים של טכנולוגיה.
גמישות התפוקה אמורה למדוד את מידע ההיענות של תפוקה לשינוי בגובה של עבודה או של הון שבהם משתמשים בתהליך הייצור. לדוגמה אם α = 0.45 הגדלה של 1% בכמות ההון שיש במפעל אמורה להגדיל את התפוקה ב-0.45%.
אם α + β = 1. אומרים שפונקציית הייצור היא בעלת החזר קבוע לגודל כך שהכפלה של ההון K ושל כמות העובדים L תוביל להכפלה של התפוקה Y. אם α + β < 1 אומרים כי יש החזר יורד לגודל, או חסרונות לגודל כך שהכפלת העובדים וההון פי 2 יניבו כמות מוצרים נמוכה מפי 2 מהמוצרים. אם α + β > 1 יש החזרים גדולים לגודל או יתרונות לגודל. יש לשים לב כי בהקשר זה יתרונות לגודל או חסרונות לגודל מתייחסים רק לתהליך הייצור ומתעלמים מהיבטים אחרים של פירמה עסקית כמו היכולת לגייס הון פיננסי (מבנקים, בעלי מניות או מוסדות הון אחרים), לבצע מינוף פיננסי, היבטים הנוגעים לשיווק, לובי פוליטי לשם שינוי לטובה של רגולציה, הטיית מכרזים, או קבלת הטבות במיסוי מטעם השלטון וכמובן היכולת לשתף פעולה עם עסקים אחרים אם במסגרת אוליגופול מול שוק הסחורות ואם בהקשרים אחרים (כמו שיתופי פעולה בין פירמות שיש להם מוצרים משלימים).
כלכלנים נאו-קלאסיים טוענים כי אם כי קיימת תחרות משוכללת (שכוללת גם הנחות כמו מידע מלא, רציונליות מלאה, העדר עלויות עסקה, ועלויות חיצוניות ועוד) וכאשר מניחים כי יש החזר קבוע לגודל אזי ניתן להראות כי α שווה לתרומה של ההון לתהליך הייצור ו-β שווה לתרומה של העובדים לתהליך הייצור.
קוב ודאגלס הושפעו על ידי נתונים סטטיסטיים שהצביעו על כך שהתרומה של עובדים ושל הון כחלק מהייצור היו קבועים על פני זמן במדינות מפותחות. הם הסבירו זאת על ידי התאמה סטטיסטית של פונקציית הייצור שלהם. כיום יש תהיה האם קבעון כזה אכן קיים.
ניתן כמובן לשכלל את משוואת קוב-דאגלס הבסיסית. לדוגמה במודלים מאוחרים יותר כלכלנים הוסיפו גורם ייצור נוסף, הון אנושי, כדי להסביר הבדלים בפריון ללא שינוי בכמות ההון התעשייתי או בכמות העובדים, ו/או שמירה של מפעלים במדינות מתועשות במקום העברה שלהם למדינות מתפתחות. כמו כן יש מודלים שניסו להוסיף גורם ייצור כמו טכנולוגיה כדי להעריך שינויים בייצור על פני זמן, אם כי דבר זה גרר בעיות (ראו ביקורת).
היסטוריה
פול דאגלס הסביר כי הניסוח הראשון של משוואת קוב-דאגלס נוסחה בשנת 1927 כאשר הוא חיפש צורה של משוואה כדי לחשב הערכות של הון ושל עובדים, הוא דיבר עם המתמטיקאי צ'רלס קוב, שהציע את הצורה Y = ALβK1−β ששימשה קודם לכן את Knut Wicksell.
הערכה של נוסחה זו בשיטת הריבועים הפחותים (least squares) דאגלס הגיע להערכה של קבוע הגמישות בתפוקה עבור עובדים שהגיע ל-0.75. מאוחר יותר הגיעה הלשכה הלאומית למחקר כלכלי (National Bureau of Economic Research) להערכה קרובה של 0.741 עבודות מאוחרות יותר בשנות ה-40 אפשרו אקספוננטים שונים ל-K ול-L והניבו תוצאות דומות למדדים משופרים של מדידת פריון שפותחו באותו זמן.
ביקורת עיקרית באותו זמן הייתה כי הערכות של פונקציית ייצור, למרות שנראו מדוייקות, היו מבוססות על מידע מועט כל כך שקשה לתת להן אמינות. דאגלס העיד כי ביקורת זו הרפתה את ידיו. פריצת הדרך בוצעה באמצעות נתונים של הלשכה לסטטיסטיקה של ארצות הברית שנגעו לסקטורים שונים, והביאו מספר גדול של תצפיות. דאגלס הציג את הממצאים כמו גם ממצאים ממדינות נוספות במאמר שלו כנשיא האגודה האמריקאית לכלכלה (American Economic Association). זמן קצר לאחר מכן נכנס דאגלס לפוליטיקה ומצבו הבריאותי התדרדר, ולכן לא קידם יותר את הנושא.
עם זאת, שני עשורים לאחר מכן, נעשה שימוש רב בפונקציית הייצור שלו שאומצה על ידי כלכלנים נאו-קלאסיים בולטים כמו פול סמואלסון ורוברט סוואלו.
משוואת קוב-דאגלס בולטת במיוחד בגלל שהיא הפונקציה הראשונה שבה השתמשו בפונקציה שפותחה במיקרו-כלכלה (לפחות בתאוריה) כדי לייצג משוואות מאקרו-כלכליות. דבר זה היווה שינוי פורץ דרך בדרך בה כלכלנים התייחסו אל מאקרו-כלכלה.
ביקורת מיקרו-כלכלית
קיימת ביקורת כלפי שימוש בפונקציית ייצור קוב-דאגלס לתיאור תהליכי ייצור במיקרו-כלכלה, מצד כלכלנים אקולוגיים וכלכלנים פוסט קיינסיאניים. וכן בשימוש בה לצורכי מאקרו-כלכלה.
העדר בסיס מיקרו -כלכלי לפונקציה
לרוב הפונקציה מוצגת כפונקציה המתאימה למפעל כלשהו. עם זאת, הפיתוח שלה נעשה לגבי נתונים מאקרו-כלכליים המתאימים למשק שלם או לגבי ענפים בכלכלה. דאגלס וקוב לא אספו נתונים של מפעל כלשהו אלא נתונים לגבי כלל התעשייה בארה"ב.[1]
התעלמות ממשאבי טבע ומאנרגיה
בשימוש בפונקציית קוב-דאגלס מניחה בדרך כלל כי שני גורמי הייצור החשובים הם הון תעשייתי ועבודה. הכלכלנים ניקולס ג'ורג'סקיו-רוגן והרמן דיילי משתמשים בניתוחים של מודל זרמים ומאגרים וניתוחים מתחומי פיזיקה וכלכלה אקולוגית וטוענים כי זו הצגה שגויה של תהליך הייצור. ללא זרם של חומר ואנרגיה שעובר דרך תהליך הייצור לא ניתן לייצר מוצרים. דאגלס וקוב עצמם העירו בסוף המאמר המקורי שלהם, משנת 1928, כי יש להתייחס ל"גורם הייצור השלישי" של "משאבי טבע" ולראות כיצד הדבר משנה את החישובים שלהם.[1] למרות הערה זו דבר זה לא בוצע על ידי רוב הספרות הכלכלית.
אם נתבונן במפעל לייצור מיץ תפוזים, אזי כמות המסחטות שיש בו (הון תעשייתי) וכמות העובדים שעובדים במפעל הם "מלאים". שעות עבודה של הפועלים מייצרים זרם של עבודה. אבל מפעל כזה לא יוכל לייצר ולו בקבוק מיץ אחד של תפוזים לא זרם של תפוזים נכנסים (חומר) ושל אנרגיה (הפעלת המסחטות בחשמל, תאורה, שינוע התפוזים, ומזון הנדרש לשמירת הפועלים בחיים ולשם הפעילות שלהם במפעל). הזרמים האלה חייבים להפוך לזרם נוסף של חומרים (בדרך כלל פסולת או חומרים בעלי אנטרופיה גבוהה יותר) ושל חום, וזאת מלבד זרם המוצרים היוצא מהמפעל. התיאור הרגיל של קוב-דאגלס סותר את החוק הראשון של התרמודינמיקה שקובע שכמות המאסה שיוצאת מהמפעל (כמות המוצרים והפסולת בתקופה נתונה) צריכה להיות זהה לכמות המאסה שנכנסת אליה. התיאור סותר גם את החוק השני של התרמודינמיקה שמתייחס לאובדן אנרגיה במהלך ייצור המוצרים.
דיילי טוען בספר לטובת הכלל כי ההזנחה של תרומת משאבי הטבע לייצור מתאימים לברית אינטרסים בין פועלים לבין בעלי הון. למראות המאבקים הרבים בין הנציגים של שני הגורמים האלה, לשניהם יש אינטרס במחירים נמוכים של תשומות שבאופן מסורתי הגיעו מצד מעמד שלישי של אצולה ו/או איכרים – מחירי קרקע נמוכים, מחירי מזון נמוכים, מחירים נמוכים של חומרי גלם ושל אנרגיה. הגורמים היחידים בייצור הם כביכול הון תעשייתי (שמסופק על ידי בעלי ההון) והעבודה (שמסופקת על ידי הפועלים). הכנסת גורמי ייצור טבעיים פנימה הייתה מורידה את "הפריון השולי" של כל גורם ייצור, ולפי התאוריה הנאו-קלאסית בשוק משוכלל כל גורם כזה מקבל תמורה (שכר או תשלום ריבית על השכרת הון) לפי תרומתו השולית לייצור- הכנסת משאבי טבע למשוואה הייתה בהכרח באה על חשבון התרומה של שני הגורמים האחרים.
הטענה של ניקולס ג'ורג'סקיו-רוגן ושל דיילי, היא למעשה רדיקלית יותר שכן מרגע שעוברים למודל זרמים ומאגרים קשה להישאר במודל כלכלי שבו תשלום השכר והריבית הוא לפי תרומה שולית לתהליך הייצור. ללא זרם מתמיד של תפוזים אי אפשר לייצר מיץ ללא תלות בכמות העובדים במפעל.
ייצור מקבילי מול ייצור סדרתי וקביעת כמות העובדים
פונקציית קוב-דאגלס מתאימה לדוגמאות של ייצור מקבילי, כמו לדוגמה פועלים הקוטפים תפוזים בפרדס, כאשר הם יכולים להיעזר בהון תעשייתי כמו סולמות ובכך להעלות את התפוקה. בייצור מקבילי התפוקה של כל פועל לא תלויה בתפוקה של שאר הפועלים. בניתוח נאו-קלאסי מסתכלים על התפוקה השולית של כל פועל וטוענים שהיא קובעת עת השכר. התפוקה עולה בהתחלה עד שכביכול מגיעים ל"תפוקה שולית פוחתת" כאשר הוספת עוד פועלים מניבה תוספת של פחות ופחות תפוזים. בנקודה מסויימת שבה התפוקה שולית שווה לעלות שולית, מתוך הנחה שהמחיר של התפוזים והמחיר של שכר הפועלים נתון על ידי השוק, אמורה פירמה תחרותית לקבוע את כמות הפועלים שברצונה להעסיק.
לעומת זאת בדוגמאות של ייצור סדרתי כמו בקו ייצור, התפוקה של פועל אחד תלויה בתוצרי הביניים של פועלים אחרים. התפוקה היא של קו ייצור שלם שבו חייבת להיות כמות מסויימת של מכונות ופועלים. הוספת עוד פועלים לקו ייצור קיים (ללא שינוי בכמות ההון) לא תגדיל את הייצור, הוספת עוד מכונות (ללא שינוי בכמות הפועלים) לא תשנה את כמות הייצור. ואפילו הוספה של כמות של מכונות ופועלים כל עוד לא הרכיבו קו ייצור שלם חדש, לא תשנה את הייצור. התיאור של ניתוח שולי לקביעת השכר לא מתאים יותר. שכן התרומה של הפועל האחרון בקו הייצור הוא התפוקה של קו הייצור כולו, ואם נוסיף עוד פועל (לדוגמה כאיש גיבוי) התרומה של פועל זה תהיה אפסית. מכאן מגיעים לפונקציית ייצור שאינה מספקת נגזרות בצורה מתמשכת ומכאן קושי להגיע לקביעת השכר של הפועלים (או תשלום של ריבית עבור מכונות) לפי פונקציית הייצור.
תיאור מתאים יותר לתהליכים סדרתיים הוא חוק המינימום של ליביג שבו תמיד יש גורם ייצור קריטי שמגביל את כמות הייצור, ותוספת של גורמי ייצור אחרים אינה מעלה כלל את רמת הייצור. הדוגמה של קו-ייצור לא רק שמתאימה לחוק זה אלא גם פועלת בצורה לא-רציפה אלא בדידה (יש צורך להוסיף כמות של כך וכך מכונות וכך וכך פועלים כדי לקבל קו ייצור חדש ועד להוספת קו ייצור כזה התוספת של פועלים ומכונות לא מעלה את כמות הייצור). תיאור מורכב יותר של תהליכים סדרתיים ותהליכים רשתיים (שיכולים לכלול מלאים של מוצרי ביניים) הוא מודל זרמים ומאגרים.
ייצור מול שיווק
לא רק שתהליך הייצור עצמו עשוי להיות סדרתי ולא מקבילי. השיווק והמכירות של מוצרים ושירותים עשויים להיות מגבלה חשובה יותר על כמות ההכנסות והרווח של המפעל או הפירמה ולא רק בתהליך הייצור. במוצרים רבים כך קיום של מכירה יכול להיעשות רק אם בוצע קודם לכן ייצור של מוצרים (לדוגמה בגדים, מזון) ו/או שייצור כזה חייב להיעשות בסמוך למועד ההזמנה (מכונית, מוצרי חשמל ואלקטרוניקה). ובכך הם הופכים את הייצור-שיווק לתהליך סדרתי. בכל מקרה מצב של שיווק ומכירות לא יכול להתקיים במשך זמן רב בצורה מקבילה לכמות הייצור.
היבט זה מדגיש כי מגבלה על מפעלים ופירמות היא לא כמות הייצור של מוצרים בתקופה נתונה אלא כמות השיווק שניתן לבצע בתקופה נתונה. הכלכלן סטיב קין טוען בספר הפרכת הכלכלה כי היבט זה יחד עם ניתוח דינאמי של מקסום רווח של פירמות יגרום לרוב הפירמות לרצות להיות במצב של עודף כושר ייצור כדי להיות מסוגלות להיענות להזדמנויות חדשות. קין טוען שהניתוח הנאו-קלאסי ממקסם רווח כאשר יש הנחה כי אין שינוי על פני זמן של הכמות המבוקשת ולכן פירמות ממקסמות רווח במודל זה בלי להתייחס לנגזרת הזמן אלא רק לנגזרות אחרות. מכאן מגיע קין לכך שפירמות שרוצות למקסם רווח לא נוהגות כמו בניתוח הנאו-קלאסי שלפיו התפוקה השולית שווה לעלות השולית.
ביקורת מאקרו-כלכלית
חסור עקביות ותרומה שלילית של ההון לייצור
הכלכלנים Jesus Felipe וF. Gerard Adams טוענים כי ביצוע רגרסיה מודרנית על הנתונים המקוריים של דאגלס, בין 1899 ל-1922, מניבה תוצאות לא עקביות. אם מריצים את הרגרסיה רק בשנים 1899-1920 מקבלים לפתע מקדמים שונים מאוד מהמקדמים שנוצרו ברגרסיה עבור כל התקופה.
בנוסף, הם מצטרפים לתמיהה של יוזף שומפטר ושל כלכלנים בולטים אחרים מהעדר ההשפעה של שינויים טכנולוגיים על גודל התוצר לאורך זמן. כאשר בודקים את המשוואה עם טכנולוגיה לגבי ההשפעה על כמות התוצר הכוללת או לגבי כמות הצמיחה הכלכלית מתקבלת תוצאה מוזרה לפיה מקדם ההשפעה של ההון על התוצר ההוא שלילי – כלומר ההון הפיזי מזיק כביכול לתוצר. תוצאה זו אינה הגיונית במיוחד, אף כי היא מופיעה בעבודות של כלכלנים רבים שעסקו בנושא.[2]
מדידת כמות ההון
 ערך מורחב – מחלוקת קיימברידג' על ההון
ערך מורחב – מחלוקת קיימברידג' על ההון
חלק ממשוואת קוב-דאגלס הוא ניסיון למדוד את כמות ההון התעשייתי שמעורבת בתהליך הייצור ומסומנת באות K. הכלכלנית ג'ואן רובינסון שאלה בשנת 1953 את השאלה הבאה – באיזה יחידות מודדים את ההון? בכך הציתה רובינסון את מחלוקת קיימברידג' על ההון. מבחינה מיקרו-כלכלית ומאקרו-כלכלית מוצרי הון הם מוצרים הטרוגניים (שונים זה מזה) שלכל אחד מהם יש מאפיינים טכנולוגיים שונים. לדוגמה כיצד מודדים את כמות ההון שיש למפעל שיש לו מספריים, טרקטור וסככה? מסיבה זו לפי רובינסון אי אפשר להציג מאגר של מוצרי הון כיישות פיזית הומוגנית.[1]
כלכלנים נאו-קלאסיים מנסים להתמודד עם בעיה זו על ידי מדידת "הערך הריאלי" של כלל המכונות הציוד והמבנים המעורבים בתהליך הייצור. גישה כזו מאומצת גם ביחס לכלל ההון התעשייתי שיש במשק במסגרת "פונקציית ייצור מצרפית".
גישה זו נתקפה על ידי רובינסון ועמיתה. הטענה היא כי מחיר ההון (של כלל ההון במשק) תלוי בשיעור- הרווח ושיעור הרווח כבר כולל, במבנה שלו, את כמות ההון. הרווח לפי התפישה הנאו-קלאסית, תלוי ב'פריון ההון', וזה האחרון הינו פרופורציונלי לכמות ההון. רובינסון טענה שיש כאן הסבר מעגלי. שכן מחיר ההון תלוי בשיעור הרווח, אלא שהרווח לפי הנאו-קלאסיים תלוי בפריון ההון וכאן נכנסים ללולאה אינסופית. רובינסון טענה כי ניתן לצרף יחד רק את הערך הכלכלי של ההון, ולכן לא ניתן להתייחס למושג של "הון" ככמות בת-מדידה שעומדת בפני עצמה בלי קשר לשאלות של מחירים ושל חלוקת הכנסות במשק.
הזנחת הון טבעי וסוגי הון אחרים
פונקציית קוב-דאגלס משמשת לעיתים קרובות גם לניתוחים של מאקרו–כלכלה. ביקורת של כלכלה אקולוגית על שימוש זה הוא על ההנחה של תחליפיות בין הון טבעי לבין הון תעשייתי ובין הון לבין עבודה וכן על תחליפיות בין אנרגיה וחומרי גלם (באנטרופיה נמוכה) לבין הון תעשייתי.
ראו גם
קישורים חיצוניים
- פונקציית ייצור קוב-דאגלס בוויקיפדיה האנגלית
- Jesus Felipe, F. Gerard Adams, “A THEORY OF PRODUCTION” THE ESTIMATION OF THE COBB-DOUGLAS FUNCTION: A RETROSPECTIVE VIEW Eastern Economic Journal, Vol. 31, No. 3, Summer 2005
הערות שוליים
- ^ 1.0 1.1 1.2 Cobb, C. W.; Douglas, P. H. (1928). "A Theory of Production". American Economic Review 18 (Supplement): 139–165.
- ^ Jesus Felipe, F. Gerard Adams, “A THEORY OF PRODUCTION” THE ESTIMATION OF THE COBB-DOUGLAS FUNCTION: A RETROSPECTIVE VIEW Eastern Economic Journal, Vol. 31, No. 3, Summer 2005