קביעת כמויות הייצור בפירמה במודל הנאו-קלאסי
|
|
התיאור הנ"ל לקוח מתוך ספרו של סטיב קין, הכלכלה במערומיה. במאמר הזה, מסביר קין את התיאור הנאו-קלאסי לדרך בה פירמה בשוק תחרותי קובעת את הכמות אותה היא תייצר. (בהמשך קין מנסה להראות מדוע תיאור זה הינו שגוי).
מבוא
התאוריה הכלכלית הנאו-קלאסית של הייצור טוענת כי מגבלות קיבולת משחקות את התפקיד המרכזי בקביעת מחירים, כשעלות הייצור - ולפיכך מחירים - עולים כשיצרנים מנסים לסחוט עוד ועוד תפוקה מתוך מספר קבוע של מכונות. לטיעון יש כמה שלבים: השלב הראשון מציב את ההנחה שהפריון יורד כשהתפוקה גדלה; שלב שני לוקח את טיעון הפריון היורד ומנסח אותו מחדש כעלויות עולות; ושלב שלישי קובע את נקודת המקסימום של הרווחיות על ידי זיהוי המקום בו קיים הפער הגבוה ביותר בין הכנסות לבין והוצאות.
שלב ראשון: פריון יורד כשהתפוקה עולה
התאוריה הכלכלית מניחה כי עקומת ההיצע משתפעת כלפי מעלה, היות והפריון יורד כאשר התפוקה גדלה. הפריון היורד הזה מתרגם למחיר עולה. לכן, יש קשר ישיר בין מה שכלכלנים מכנים 'פריון שולי' (או תפוקה שולית)- הכמות שמיוצרת על ידי העובד האחרון - ובין ה-'עלות השולית' - העלות של ייצור היחידה האחרונה.
טבלה 1 מציגה דוגמה לדרך בה תופסים כלכלנים את היצור. הפירמה הדימיונית הינה בעלת הוצאות קבועות של 250,000 דולר ומשלמת לעובדיה שכר של 1,000 דולר. היא יכולה למכור כמה מוצרים שהיא מסוגלת לייצר במחיר השוק של 4 דולר. כדי לייצר תפוקה בכלל, על הפירמה לגייס עובדים: ללא עובדים, התפוקה היא אפס. העובד הראשון מאפשר לפירמה לייצר 52 יחידות תוצרת. ניתן לראות זאת בשורה הראשונה בטבלה: מספר העובדים הוא יחידה אחת, סך התפוקה היא 52 יחידות.
התוצר השולי של העובד - ההבדל בין התפוקה בלעדיו\בלעדיה (אפס) לבין התפוקה איתו - הוא 52 יחידות. המחיר השולי של התפוקה הוא המשכורת של העובד -1,000 דולר- אם נחלק זאת במספר היחידות שנוצרו - 52 - נקבל את העלות השולית בסך 19.20 דולר.
העלויות הקבועות הממוצעות של התפוקה בנקודה זו הינן עצומות- 250,000 דולר חלקי 52, או 4,807 דולר. העלות הממוצעת הכוללת היא 251,000 דולר חלקי 52, או 4,827 דולר ליחידה - דבר שמשמעותו הפסד של 4,823 דולר לכל יחידת תוצר שנמכרת, אם זו רמת התפוקה שתיבחר.
טבלה 3.1 מידע על הוצאות והכנסות של פירמה היפותטית
| עובדים | תפוקה | שכר כולל | עלות כוללת | תוצר שולי | עלות שולית |
עלות קבועה ממוצעת |
עלות משתנה ממוצעת |
עלות כוללת ממוצעת |
הכנסה | רווח |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 52 | 1,000 | 251,000 | 52.0 | 19.2 | 19 | 4,808 | 4,827 | 208 | 250,792- |
| 9 | 611 | 9,000 | 259,000 | 83.6 | 12.0 | 15 | 409 | 424 | 2,444 | 256,556- |
| 10 | 698 | 10,000 | 260,000 | 87.5 | 11.4 | 14 | 358 | 372 | 2,792 | 257,208- |
| 100 | 23,333 | 100,000 | 350,000 | 398.5 | 2.5 | 4 | 11 | 15 | 93,332 | 256,668- |
| 276 | 131,111 | 276,000 | 526,000 | 772.5 | 1.3 | 2 | 2 | 4 | 524,444 | 1,556- |
| 277 | 131,885 | 277,000 | 527,000 | 773.7 | 1.3 | 2 | 2 | 4 | 527,540 | 540 |
| 400 | 233,333 | 400,000 | 650,000 | 850.0 | 1.2 | 2 | 1 | 3 | 933,332 | 283,332 |
| 500 | 316,667 | 500,000 | 750,000 | 800.5 | 1.2 | 2 | 1 | 2 | 1,266,668 | 516,668 |
| 700 | 443,333 | 700,000 | 950,000 | 401.5 | 2.5 | 2 | 1 | 2 | 1,773,332 | 823,332 |
| 725 | 452,370 | 725,000 | 975,000 | 323.5 | 3.1 | 2 | 1 | 2 | 1,809,480 | 834,480 |
| 730 | 453,938 | 730,000 | 980,000 | 307.1 | 3.3 | 2 | 1 | 2 | 1,815,752 | 835,752 |
| 735 | 455,424 | 735,000 | 985,000 | 290.5 | 3.4 | 2 | 1 | 2 | 1,821,696 | 836,696 |
| 740 | 456,827 | 740,000 | 990,000 | 273.7 | 3.7 | 2 | 1 | 2 | 1,827,308 | 837,308 |
| 746 | 458,144 | 745,000 | 995,000 | 256.6 | 3.9 | 2 | 1 | 2 | 1,832,576 | 837,576 |
| 746 | 458,397 | 746,000 | 996,000 | 253.1 | 4.0 | 2 | 1 | 2 | 1,833,588 | 837,588 |
| 747 | 458,647 | 747,000 | 997,000 | 249.7 | 4.0 | 2 | 1 | 2 | 1,834,587 | 837,587 |
| 748 | 458,893 | 748,000 | 998,000 | 246.2 | 4.1 | 2 | 1 | 2 | 1,835,572 | 837,572 |
| 800 | 466,667 | 800,000 | 1,050,000 | 52.0 | 19.2 | 2 | 1 | 2 | 1,866,668 | 816,668 |
בשלב זה, נהנה היצור מיתרון לגודל. עובד יחיד היה צריך לבצע את כל הפעולות, בעוד שעובד שני מאפשר לחלק את המשימות בינם, כך שכל אחד מהם מתמחה לפחות במובן זה. עם ההתמחות, גדל הפריון של שני העובדים. התהליך חוזר על עצמו עם העובד ה-9 וה-10, כך שהתפוקה השולית של העובד ה-9 - הכמות שהוא מוסיף לתפוקה מעל לכמות שיוצרה על ידי 8 עובדים - היא 83.6 יחידות. באופן דומה, התפוקה השולית של העובד העשירי היא 87.5 יחידות תוצר.
אם הפירמה אכן מייצרת כמות מוצרים בהתאם, היא תפסיד 257,207 דולר - יותר מהעלויות הקבועות שלה. עם זאת, התהליך של פריון שולי עולה - ולפיכך ירידה של העלות השולית - בא להצלה כאשר התפוקה גדלה. עם 100 פועלים, הפירמה עדיין מפסידה, אבל ההפסד יורד בגלל שהתפוקה השולית ירדה מתחת למחיר המכירה של המוצר בשוק. העובד ה-100 מוסיף 398.5 יחידות לתוצר, בעלות שולית של 1,000 דולר חלקי 398.5, או רק 2.5 דולר ליחידה. זה פחות מאשר מחיר המכירה של 4 דולר ליחידה, כך שהפירמה מרוויחה על הגידול בתפוקה - אבל בשלב זה, היא רק מקטינה את ההפסדים שלה, ולא עוברת מהפסד לרווח.
רווח כולל מגיע עם העובד ה-227, שמביא לתוספת רווח של 3,090 דולר - התוצאה של מכירת 772.5 יחידות נוספות במחיר 4 דולר ליחידה - בעבור עלות שכר של 1,000 דולר. התהליך הזה של עליה בתפוקה השולית ממשיך עד לשכירת העובד ה-400. בשלב הזה, העלות השולית ירדה באופן משמעותי. העובד ה-400 מוסיף 850 יחידות לתפוקה, כך שהעלות השולית של התפוקה שלו היא השכר של 1,000 דולר מחולק ב-850, או 1.18 דולר (מעוגל ל-1.2 דולר בטבלה). העלויות הקבועות הממוצעות, שהיו עצומות ברמות המזעריות של התפוקה, הן זניחות יחסית ברמת הייצור של 233,333 יחידות תוצר: הן ירדו לדולר אחד.
מנקודה זו והלאה, הפריון של כל עובד חדש מפסיק לעלות. כל עובד חדש מוסיף פחות לתפוקה ביחס לקודמו. ההיגיון הוא שיחס העובדים - 'גורם היצור המשתנה' - למכונות - 'גורם היצור הקבוע' עבר איזושהי רמה אופטימלית. כעת כל עובד חדש עדיין מוסיף לתפוקה, אבל בקצב קטן והולך. במונחים כלכליים, הגענו לאזור שבו שוררת תפוקה שולית פוחתת. היות וכעת והתוצר השולי יורד, העלות השולית תתחיל לעלות.
אבל הרווח ממשיך לעלות, שכן למרות שכל עובד חדש מוסיף פחות תפוקה, ולכן מניב פחות הכנסה, ההכנסה מיחידות המוצר הנוספות עדיין עולה על העלות של שכירת העובד. בז'רגון כלכלי, ההכנסה השולית עולה על העלות השולית.
אנחנו יכולים לראות זאת אם נתבונן בעובד ה-500, שמוסיף 800.5 יחידות לתוצר. העלות השולית של התפוקה שלו היא השכר (1,000 דולר) מחולק ב-800.5, או 1.25 דולר (מעוגל למטה בטבלה). זה גבוה יותר מהמינימום של 1.18 דולר אליו הגענו עם העובד ה-400. אבל כל יחידות המוצר הנוספות שהעובד הזה מייצר יכולות להימכר ב-4 דולר האחת, כך שהפירמה עדיין מרוויחה מהעסקת העובד ה-500.
אותו עקרון עובד עדיין עבור העובד ה-600, וה-700. הפריון נופל במהירות כעת, כך שעובד זה מוסיף רק 401.5 יחידות לתפוקה, עבור עלות שולית של 2.5 דולר אבל זה עדיין נמוך יותר ממה שמתקבל ממכירת התוצרת הנוספת.
תהליך זה של רווח עולה מגיע לקיצו עם העובד ה-747, שהתוצר הנוסף שלו - 249.7 יחידות - יכול להימכר רק עבור 998.8 דולר, לעומת עלות השכר שלו של 1,000 דולר. מנקודה זו והלאה, כל עובד נוסף עולה יותר מאשר ההכנסה הנובעת מכירת תוספת התפוקה שלו.
לכן הפירמה צריכה להעסיק 746 עובדים, ולמקסם את הרווח שלה ל-837,588 דולר. בנקודה זו, העלות השולית של הייצור שווה להכנסה השולית מהמכירות, והרווח הוא מקסימלי.
העובד ה-800 מוסיף 52 יחידות תוצר, עבור עלות שולית שנוסקת כעת ל-19.20 דולר. כשאנו מגיעים לעובד ה-812, העובדים - באופן מטפורי- נופלים זה מעל זה על רצפת המפעל, ועובד זה מוסיף רק 3.3 יחידות לתוצר, בעלות שולית של 300 דולר. העובד הבא למעשה מוריד את התפוקה.
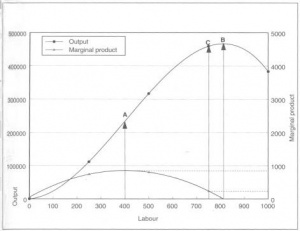
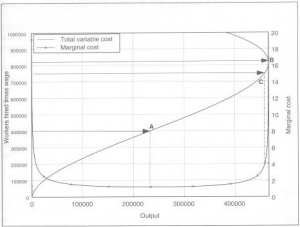
התרשימים הבאים מציגים את הטבלה בצורה גרפית. בתרשים 1 כמות העובדים מוצגת בציר האופקי, התפוקה בציר האנכי השמאלי (בסולם מאפס עד 500,000) והתפוקה השולית בציר האנכי הימני (עם סולם מאפס עד - 5,000 אבל רק התחום התחתון, עד 1,000, הוא רלוונטי). כפי שאפשר לראות בטור החמישי של טבלה 1, התפוקה השולית - התפוקה שנוצרת על ידי כל עובד חדש - עולה במשך זמן מה. היא מגיעה לשיא בעובד ה-400, שמוסיף 850 יחידות לתוצר (מוצג על ידי הקו המקווקו שמגיע לציר האנכי הימני בנקודה שקו A חותך את העקומה התחתונה). מנקודה זו והלאה, השיפוע של עקומת התפוקה מתחיל לרדת. עד שנגיע לעובד ה-813 נגיע לרמה המקסימלית האפשרית של תוצרת, נקודה B. כאן התפוקה השולית של העובד האחרון היא כמעט אפס, והתפוקה השולית של העובד הבא היא למעשה שלילית.
שלב שני: פריון יורד משמעו עלויות עולות
כלכלנים בדרך כלל נחפזים ישירות אל תוך טיעון זה בספרי הלימוד שלהם, אבל אני אבצע את המעבר משלב הראשון לשלב השני בצורה איטית, כדי להדגיש את הנקודה שעבור כלכלנים, הכל נקבע על ידי תפוקה שולית יורדת.
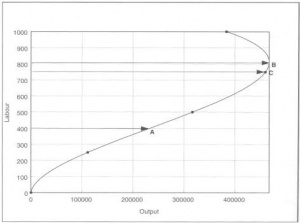
הצעד הראשון בתהליך זה הוא תרשים 2, שפשוט מחליף את הצירים מתרשים 1. במקום שהתשומה של העבודה הייתה על הציר האופקי והתפוקה על הציר האנכי בתרשים 1, התפוקה בתרשים 2 היא על הציר האופקי והתשומה של העבודה הינה על הציר האנכי. בחרו כל רמה של תפוקה על הציר האופקי של תרשים מספר 2, והציר האנכי יגיד לכם כמה עובדים נדרשים כדי לייצר אותה.
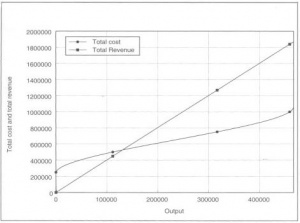
בהמשך, אנו ממירים את הציר האנכי בתרשים 2 ממידה של עבודה למידה של עלויות משתנות. כדי לעשות זאת, כל שעלינו לעשות הוא להכפיל את תשומת העבודה בשכר. היות ובדוגמה שלנו השכר הוא 1,000 דולר, כל המספרים על הצרי האנכי בתרשים 3 גדולים פי 1,000 מהמספרים בתרשים 2.
היות והציר האנכי בתרשים 3 הוא במונחים כספיים, אנו יכולים להוסיף לו עוד נתונים כספיים. ברור מאליו שיש להוסיף את העלויות הקבועות של הייצור - 250,000 דולר - אל העלויות המשתנות שנראות בתרשים 3, כך שעקומת העלויות מראה כעת את סך העלויות, במקום רק את העלויות המשתנות. מה שלא כל כך ברור מאליו הוא שאנו יכולים כעת להתקדם לשלב שלוש של הטיעון, על ידי הוספה של סך ההכנסה שהפירמה מרוויחה ממכירת מוצריה. היות והנחנו שהפירמה יכולה למכור כמה שהיא רוצה עבור 4 דולר ליחידה, זה יהיה קו ישר דרך ראשית הצירים עם שיפוע של 4: 4 דולר של הכנסה לכל יחידה אחת שנמכרת.
שלב שלישי: קביעת הנקודה של רווחיות מקסימלית
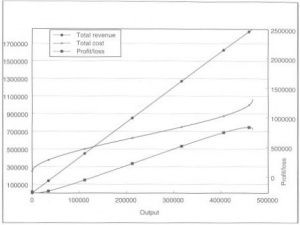
הרווח המקסימלי של הפירמה ימצא בנקודה בה יהיה המרווח (החיובי) הגדול ביותר בין הקו הישר של פונקציית ההכנסה שלה לבין עקומת פונקציית העלות הכוללת. דבר זה מצוייר בתרשים 4, שמאפשר לנו לזהות את רמת התפוקה האידאלית מבחינה כלכלית עבור הפירמה - אבל עדיין לא קל לזהות אותה מבחינה וויזואלית. זה מתרחש היכן שהשיפוע של עקומת ההכנסה הכוללת משתווה לשיפוע של עקומת ההוצאה הכוללת, היות וזה מניב את המרווח הגדול ביותר בין ההכנסה הכוללת לבין העלות הכוללת.
דבר זה מתקיים היות וכאשר עקומת ההכנסות עולה בקצב תלול יותר מאשר עקומת ההוצאות, ומכירה נוספת תגרום לפער גדול עוד יותר. כאשר עקומת העלויות עולה בקצב תלול יותר מאשר עקומת ההכנסות, מכירה נוספת תקטין את הפער בין הכנסות להוצאות. לפיכך הפער הגדול ביותר מתרחש כאשר השיפוע של שתי העקומות הוא שווה. דבר זה מוצג בשרטוט של הרווח הכולל בתרשים 4. אם תבדקו את טבלה 1, תוכלו לראות שעמודת הרווח מגיעה למקסימום של 837,588 דולר ב-746 עובדים. אותו המקסימום נראה גם בתרשים 4 בקצה צד ימין של עקומת הרווח (והגרף יורד מטה מאוד מהר לאחר מכן).
בעוד שהגרף הזה אכן אומר לנו את רמת התפוקה שבה הרווח מגיע למקסימום, כלכלנים מעדיפים למצוא את הנקודה של רווח מקסימלי על ידי עבודה במונחים של השיפועים של עקומות העלות וההכנסה - העלות השולית וההכנסה השולית - במקום עם העקומות עצמן.
קל לחשב את השיפוע של עקמות ההכנסות בדוגמה זו: זה פשוט המחיר של 4 דולר ליחידה שנמכרת (במונופול הדבר מסובך יותר, אבל נשאיר את הבעיה הזאת לפרק 4). לא קל לחשב את השיפוע של עקומת העלות הכוללת מאיזשהו תרשים קודם, היות והוא שווה לשינוי בעלות חלקי השינוי בתפוקה, אבל חישבנו את זה בטבלה 1, כך שמספרים אלו משמשים לייצר את שני התרשימים הבאים. העלות הכוללת והעלות השולית מוצגות בתרשים 5, כשנקודות A ,B, ו-C מוצגות שוב לשם תזכורת. זכרו שנקודה A, שבה מועסקים 400 עובדים, נתנה את התפוקה השולית הגבוהה ביותר ולכן את העלות השולית הנמוכה ביותר - תוכלו לראות זאת בציר האנכי הימני של התרשים. תוכלו גם לראות שנקודה C שבה מועסקים 746 עובדים, היא בעלת עלות שולית של 4 דולר - ששווה לעלות המכירה.
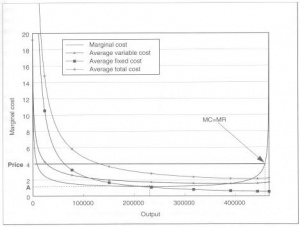
לבסוף, בתרשים 6 אנו יכולים לשרטט את הדיאגרמה הסטנדרטית בה משתמשים כלכלנים כדי לייצג את ההתנהגות של פירמה. בנוסף להצגתן של עלות שולית והכנסה שולית, תרשים 6 מציג גם: עלות קבועה ממוצעת, שמתחילה ממקום גבוה מאוד ונופלת בצורה חלקה לעבר האפס ככל שהתפוקה עולה; עלות משתנה ממוצעת, שנופלת בתחילה כאשר הפריון עולה, אבל מתחילה לעלות מרגע שהעלות השולית עולה על העלות הממוצעת; ועלות כוללת ממוצעת, שמשלבת את העלות הקבועה הממוצעת והעלות המשתנה הממוצעת. השיפוע של עקומת ההכנסות נקרא הכנסה שולית, בעוד השיפוע של עקומת ההוצאות נקרא העלות השולית.
הנקודה בה נפגשות שתי העקומות השוליות מתאימה לנקודה שבה קיים המרחק הגדול ביותר בין ההכנסה הכוללת לבין ההוצאה הכוללת. הגענו לנירוונה הכלכלית: חברה תחרותית מושלמת (המושג של 'תחרות מושלמת' או 'תחרות משוכללת' נדון בפירוט בפרק 4) מייצרת כמות שבה העלות השולית שווה הן להכנסה השולית והן למחיר.
תרשים שונה
סטודנטים לכלכלה ישימו לב שתרשים 6 שונה למדי מהתרשים הנורמלי שמצוייר בספרי הלימוד לכלכלה: עקמות העלות השולית עולה בקצב הרבה פחות תלול בגרפים של ספרי הלימוד הסטנדרטיים מאשר כאן, ואילו העלות הממוצעת עולה בקצב תלול הרבה יותר בתרשימים של ספרי הלימוד, מרגע שעלות השולית עברה אותה.
הבדלים אלו נובעים מכך שהתרשימים בספרי הלימוד הרגילים הם פשוט סקיצה שצוירה על ידי אמן גרפיקה, בעוד שתרשים 6 (והטבלה שממנה הוא נוצר) נוצרו שניהם על ידי נוסחה מתמטית פשוטה שיצרה פריון שולי שעולה בתחילה ויורד בהמשך.
הציור הכלכלי הרגיל הוא ללא ספק יותר אסתטי, אבל הוא מבוסס באופן פחות טוב על התאוריה הכלכלית מאשר התרשימים בפרק זה. הדרך היחידה בה עלות שולית יכולה לעלות באופן כה מתון כמו בספרי הלימוד ועם זאת שהעלות הממוצעת תעלה באופן כה תלול, היא אם הכמויות שמיוצרות הן יחסית קטנות - בסדר גודל של עשרות יחידות, בהשוואה למאות האלפים שבהם השתמשנו בתרשימים שלנו (נושא זה נדון ברשת ב-Size/Maths). במובן זה התרשימים של ספרי הלימוד הרגילים הינם דוגמה קלאסית של האיכות בסגנון אשר של תרשימים רבים של הכלכלה הסטנדרטית: הם מציגים מה אפשר לצייר, במקום מה באמת אפשר לקבל מתוך התאוריה.
מדגי הרקק אל השוק
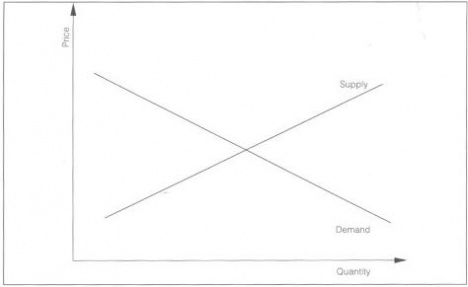
האקספוזיציה למעלה מתארת פשוט את המצב עבור פירמה בודדת. כדי להגיע לעקומת ההיצע של השוק, עלינו לסכום את עקומת ההיצע של מספר רב של יצרנים - פשוט כאילו אנחנו משלימים את הדרך בה הגענו לחישוב עקומת הביקוש של השוק, עקומת הביקוש של המוני צרכנים שנצברו יחדיו. עקומת ההיצע הכוללת מתקבלת פשוט על ידי חיבור כל עקומות העלויות השוליות של פירמות בשוק תחרותי. היות ועקומת העלות השולית של כל פירמה בודדת עולה למעלה, גם עקומת ההיצע של השוק משתפעת כלפי מעלה: אנו מגיעים לעקומת ההיצע הקלאסית של השוק שנראית בתרשים 7.
ראו גם
- פרק 3 של הספר הכלכלה במערומיה, סטיב קין. בפרק מוסברת הביקורת של סראפה על התיאור הנ"ל של הייצור