דיילי: כלכלה אקולוגית, פרק 4, חוקי התרמודינמיקה

כלכלה אקולוגית: עקרונות ויישומים מאת הרמן דיילי

1. מבוא לכלכלה אקולוגית

2. האקוסיסטמה המכילה והמקיימת - הַשׇלֵם.

3. מיקרו-כלכלה

4. מאקרו-כלכלה

5. גלובליזציה

6. מדיניות

הכלכלה האקולוגית אמורה להראות לנו מתי התועלת מהצמיחה המתמדת משתווה לנזק. כדי לדעת זאת, על הכלכלנים האקולוגיים להבין את יחסי הגומלין בין הכלכלה לאקו-סיסטם וכן לפתח כלי מדיניות לשמור על הכלכלה במסגרת המקיימת.

הכלי שבו משתמשים הכלכלנים לבצע אופטימיזציה הוא השוק, אך השוק לא יכול לפעול על טובין שאינם בבעלות בלעדית של מישהו. לכן, כלכלנים אקולוגיים חייבים לפתח מנגנונים אלטרנטיביים, ולשם כך עליהם קודם כל להבין היטב את התכונות של הטובין והשירותים שאותם יש לחלק (כזכור, זהו טיבה של הכלכלה).

פלנטה סופית

בכדור הארץ כמות סופית של מים, שטחי אדמה, מינרלים ודלקים מחצביים. אמנם אנרגיה אנו מקבלים מהשמש באופן רציף, אך קצב הגעת האנרגיה גם הוא סופי. גם אנרגיה זו אנו יכולים לנצל רק אחרי שהיא הוטמעה (כמעט רק...) בתהליך פוטוסינתזה.

אך אל מול הסופיות הזו של המשאבים, צמיחה מתמדת היא המטרה של רוב הכלכלנים והמדינאים. כלכלנים רבים אף טוענים שצמיחה היא תנאי לשמירה על הסביבה: רק עשירים ושבעים יכולים להרשות לעצמם לדאוג לסביבה. כהוכחה הם מביאים את השיפור בפרמטרים סביבתיים בארצות הברית ואירופה בעשורים האחרונים. אך שיפור זה נובע בחלקו מייצוא תעשיות מזהמות או פסולת מזוהמת אל העולם השלישי, אשר מזדהם משירותים ומוצרים אשר נצרכים בעולם הראשון) - ראו עקומת קוזנץ הסביבתית.

המשאבים הסופיים של הפלנטה לא מאפשרים צמיחה לאין קץ – למשל גידול אוכלוסייה של 1% בשנה תביא את מאסת האנושות להיות גדולה ממאסת כדור הארץ תוך 3,000 שנה... יש כאלו האומרים שהמדדים הכלכליים לא מודדים בהכרח כמויות פיזיקליות, לכן המגבלות הפיזיקליות לא תופסות על הספרה הכלכלית. אך כיום הצמיחה קשורה באופן הדוק לייצור ושימוש במשאבים – אפילו שירותים דורשים משאבים עבור העובדים מספקי השרות, ובכך מעמיסים את האקו-סיסטם.

אם נשכיל לחבר את הערך הכלכלי לאיזה מושג ('זרם') של שביעות רצון נפשית, ונלמד להגדיל אותה ללא הגדלת הצרכים הפיזיקליים, אז באמת נוכל ליצור צמיחה אינסופית. הבעיה היא שכלכלת השוק הנוכחית לא מסוגלת לטפל בשביעות רצון שאינה קשורה בטובין חומריים...

כעת נסקור את התאוריה המדעית הרלוונטית לחקר הצמיחה במערכת סגורה: התרמודינמיקה.

חוקי התרמודינמיקה

בסוף המאה ה-18, עם התפתחות מנועי הקיטור, נחקרו הפרמטרים הנוגעים ליכולת ניצול האנרגיה לביצוע עבודה מכנית.

החוק הראשון של התרמודינמיקה

ראשית נמצא כי אנרגיה לא יכולה להיהרס או להיווצר יש מאין, היא רק יכולה לשנות צורה. שנית נמצא שוויון בין אנרגיה לעבודה. כך נוסח החוק הראשון של התרמודינמיקה:

U = Q – W∆

Q: כמות החום שנכנסת למערכת (יש לזכור שדובר בזמנו על מנועי קיטור, כמובן שיש לכלול ב-Q את כל אנרגיה שנכנסת למערכת), אם יוצאת מהמערכת אנרגיה, Q יהיה שלילי.
W: העבודה הנעשית על ידי המערכת. אם מבצעים עבודה על המערכת, W תהיה שלילית (למשל מקרר המשתמש במנוע להפעלת המדחס מקבל עבודה שלילית מהמנוע).
∆U: שינוי האנרגיה הפנימית של המערכת (למשל במנוע בעירה פנימית הדלק הנשרף משנה את האנרגיה הפנימית שלו ובכך מאפשר לבצע עבודה).

במצב פשוט, בו אין שינוי במצב הפנימי של המערכת, מתקיים:

Q = W

דהיינו כמות החום שנכנסת למערכת שווה לעבודה שנעשית על ידי המערכת. ניסוח זה מתיישב עם המשמעות הפיזיקלית של 'אנרגיה' שהיא "היכולת לבצע עבודה".

החוק השני של התרמודינמיקה

אך מה הופתעו החוקרים למצוא שיש גבול ליכולת לנצל אנרגיה לביצוע עבודה.

היה זה הצרפתי סאדי קרנו שניסה לחשב את היעילות של מנועי קיטור. קרנו ניסח מודל של מכונה אידאלית המשתמשת בחום כדי לבצע עבודה ('מכונת קרנו'). בחישוביו מצא קרנו כי יש מגבלה ליעילות (כמות האנרגיה ההופכת לעבודה מתוך האנרגיה המושקעת) ולעולם לא תהפוך כל האנרגיה המושקעת לעבודה – ואם המכונה האידאלית מוגבלת, ברור שכל מכונה מעשית תספק ביצועים גרועים יותר.

נמצא כי:

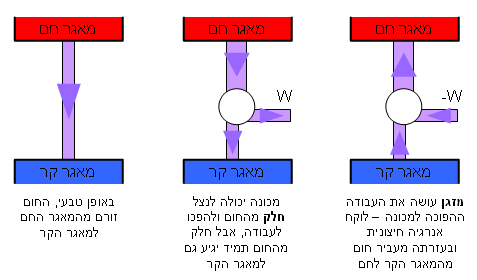
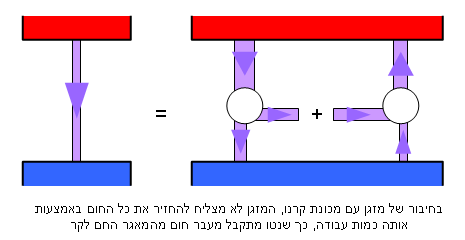
כדי לבצע עבודה יש להשתמש בשני 'מאגרי' חום – מאגר חם ומאגר קר, כאשר החום (אנרגיה) עובר באופן ספונטני מהמאגר החם אל המאגר הקר. אך לא להפך.
לא ניתן לנצל את כל האנרגיה לביצוע עבודה, חלק מהחום חייב להגיע למאגר הקר.

המסקנה היא שבכל פעם שאנו מבצעים עבודה, אנו מעבירים חום מהמאגר החם לקר, בכך מקררים את המאגר החם ומחממים את הקר. בסופו של דבר יגיעו כל המאגרים לטמפרטורה אחידה. זהו מצב של שיווי משקל תרמודינמי שבו אין שום אפשרות לבצע עבודה. כשכל מאגרי החום ביקום יגיעו לשיווי משקל תרמודינמי יגיע המוות התרמודינמי של היקום.

אנטרופיה

האנטרופיה היא מידת השינוי בפיזור האנרגיה בתהליך תרמודינמי. ככל שהאנטרופיה גבוהה יותר, כך פיזור האנרגיה גדול יותר, כך שקשה יותר לנצל אותה לעבודה. מכאן שהאנטרופיה היא מידה של האנרגיה הלא זמינה לביצוע עבודה.

למשל, בבנזין יש אנרגיה כימית. כשאנו מניעים מנוע חלק מהאנרגיה הופך לעבודה וחלק מתפזר כחום, רעש, רעידות וכד'. ניתן להשתמש בחלק מהאנרגיה הזו (למשל קו-גנרציה משתמשת בחום כדי לבצע עבודה מועילה כגון ייצור חשמל), אך ככל שהיא יותר מפוזרת כך קשה יותר לנצלה (למשל, לנצל את הרעידות לביצוע עבודה...). התגלית של קרנו הייתה שכמות מסוימת של האנרגיה בלתי אפשרי לנצל. זו אינה בעיה טכנולוגית – גם בתנאים אידאליים לחלוטין אי אפשר יהיה לנצל את האנרגיה הזו.

התאוריה הקינטית של הגזים

אחד משיאי ההתפתחות של המדע התאורטי היה ההסבר של התרמודינמיקה על ידי התאוריה הקינטית של הגזים. בסוף המאה ה-19 הצליחו (במקביל) ג'יימס מקסוול הבריטי ולודוויג בולצמן האוסטרי לגזור את חוקי התרמודינמיקה מחישוב ההתנהגות הסטטיסטית של מספר גדול של מולקולות בגז.

הם הניחו שהמולקולות בגז מתנהגות ככדורים אלסטיים, וכן הניחו את התפלגות האנרגיה בין המולקולות השונות, ובאמצעות חישובים מכאניים וסטטיסטיים הצליחו לגזור את חוקי התרמודינמיקה. זה היה ניצחון אדיר למדע התאורטי היות והוא הראה כיצד ניתן לבצע רדוקציה של תאוריה מאקרוסקופית לתורה האטומית. יש לציין שלפחות 30 שנה לאחר מכן התורה האטומית עדיין הייתה שנויה במחלוקת.

על פי ניסוח זה האנטרופיה היא מדד מסוים לאי-הסדר במערכת. האנטרופיה סופרת את מספר ה'סידורים' של המולקולות המתאימים למצב מסוים. נדגים זאת באמצעי מוכר מחיי היום יום: מה מידת ה"אנטרופיה" של החדר שלנו כשהוא מסודר וכשהוא מבולגן?

השאלה, אם כן, היא בכמה צורות אפשר לסדר חדר? יחסית מעט – הנעליים תמיד תהיינה על הריצפה, או בארון. הבגדים יהיו מקופלים בארון, הספרים מונחים על המדף. אמנם ניתן להחליף את סדר הבגדים בארון, או לשים חלק מהספרים על השולחן, אבל זה כאין וכאפס לעומת מספר הקונפיגורציות בהן יהיה החדר במצב מבולגן. על פי הניסוח הסטטיסטי האנטרופיה קשורה למספר המצבים האפשריים, כך שה"אנטרופיה" של חדר מבולגן גבוהה בהרבה מזו של חדר מסודר. יש להדגיש כאן שמדובר במשל. האנטרופיה, כמושג כימי ופיזיקלי היא זהה הן בחדר מבולגן והן בחדר מסודר, החפצים בחדר מקבילים למולקולות בחתיכת חומר כלשהי. וגם בחומר, יש הרבה יותר דרכים לסדר מולקולות במצב "מבולגן", לדוגמה מולקולות של טיפת צבע בתוך מולקולות של מים כוס מים, לעומת המצב של מים נפרדים וצבע נפרד.

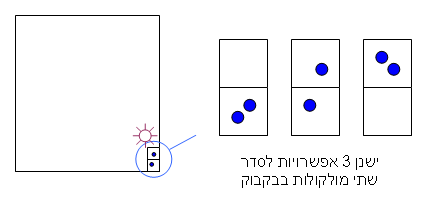
נדגים באופן דומה בעזרת מיכל ובו שתי מולקולות. כדי לספור את המצבים יש 'לחתוך' את החלל לקוביות ולספור בכמה קונפיגורציות אפשר למצוא את המולקולות בתוך הקוביות. נניח ששתי המולקולות נמצאות בבקבוק התופס שתי 'קוביות' במיכל. סה"כ ישנן 3 אפשרויות לסדר את שתי המולקולות בתוך הבקבוק (בהנחה שאי אפשר להבדיל ביניהן):

אך אם נפתח את הבקבוק וניתן למולקולות להתפזר ברחבי המיכל, יש מספר גדול בהרבה של מצבים בהם הן תוכלנה להימצא: אם צלעות המיכל הן 4x4x4 קוביות, יש כ-2,000 אפשרויות סידור, לשלוש מולקולות באותו המיכל יש יותר מ-100,000 קונפיגורציות אפשריות! מכאן שלמצב בו המולקולות בבקבוק יש אנטרופיה נמוכה, ואילו למולקולות המפוזרות במיכל אנטרופיה גבוהה (האנרגיה הקינטית של המולקולות מפוזרת כעת הרבה יותר). כעת נבצע את הניסוי הבא: נניח את הבקבוק עם שתי המולקולות בפינת החדר ונפתח את הפקק. לאחר זמן מה סביר להניח שהמולקולות תשוטטנה להן ברחבי החדר. כך המערכת עברה באופן ספונטני ממצב של אנטרופיה נמוכה (המולקולות בבקבוק) לגבוהה (המולקולות בחדר) - האנטרופיה קשורה להסתברות המערכת להימצא במצב מסויים, ככל שהאנטרופיה גבוהה יותר, ההסתברות גבוהה יותר.

מכאן אנו מגיעים לניסוח אקוויוולנטי לחוק השני של התרמודינמיקה: במערכת סגורה, האנטרופיה לעולם אינה קטנה, או אי הסדר לעולם אינו קטן, או פיזור האנרגיה לעולם אינו קטן (מה זה אומר לגבי החדר שלנו?)

חשוב לזכור שמדובר במערכת סגורה (מערכת שאינה מחליפה חומר או אנרגיה עם סביבתה), היות ובמערכת פתוחה תמיד אפשר 'לייצא' את האנטרופיה החוצה או 'לייבא' אנרגיה מבחוץ, ובעזרתה להקטין את אי הסדר. יש לזכור שניתן להשתמש באנרגיה כדי לצמצם את האנטרופיה, אך צמצום זה קטן מתוספת האנטרופיה שנגרמת כשמנסים לייצר את האנרגיה הזו. כך שאם מתייחסים יחד לשתי המערכות, מקבלים גידול נטו באנטרופיה.

נשים לב שבניסוח הזה החוק הוא בעירבון מוגבל מאוד: אם נחכה מספיק זמן (במערכת מספיק מורכבת מדובר במיליארדי פעמים גיל היקום...) נמצא לבסוף את המולקולות חזרה בתוך הבקבוק. כך שניתן לחזור באופן ספונטני ממצב בעל אנטרופיה גבוהה לנמוכה, אבל ההסתברות לכך היא מאוד מאוד מאוד נמוכה.

מכאן גם אפשר לגזור את הקשר בין האנרגיה החופשית לאנטרופיה: אם נשים טורבינה קטנה ליד פתח הבקבוק ונתפתח אותו, המולקולות יכו בטורבינה, יסובבו אותה ויאפשרו לנו לנצל את האנרגיה, אך מרגע שהמולקולות התפזרו בחדר אין לנו יותר אפשרות לנצל את תנועתן לביצוע עבודה. כך, ככל שהאנטרופיה גבוהה יותר, היכולת לבצע עבודה קטנה.

חשוב לציין מספר נקודות:

כל נושא החוק השני הוא בעייתי. פילוסופים ופיזיקאים יושבים על המדוכה בעניינו עד היום. למשל, ניתן לראות שיש קשר עמוק בין אנטרופיה ואינפורמציה (ישנו תחום שלם – תורת האינפורמציה של שנון העוסק באנטרופיה של מידע, שיטות הדחיסה דוגמת ZIP מבוססות עליה). האנטרופיה עצמה נובעת מהמידע החלקי שיש לנו אודות המציאות ברמה המיקרוסקופית. אם כן, בהינתן מידע מלא היינו יכולים לעקוף את החוק השני? (בספרות הדיון נקרא: 'השדון של מקסוול').
מעמדו של החוק השני בעייתי. יש הרואים בו חוק טבע יסודי, יש הרואים בו חוק הנגזר מהסטטיסטיקה, ויש שכלל לא מכירים בקיומו. מסתורין כבד אופף את המהלך בו נובע חוק א-סימטרי בזמן (האנטרופיה רק גדלה) מחוקים יסודיים יותר הסימטריים בזמן. מבחינה טכנית המהלך הזה נובע מהחלוקה של המרחב לקופסאות - מהלך תאורטי לחלוטין שאין לו שום משמעות פיזיקלית...
האם החוק השני תקף גם לגבי חומר? לכאורה גם בשימוש בחומר יש בלאי, שחיקה, וירידה באיכות. כך, למשל, הפלסטיק המופק מבקבוקים ממוחזרים הינו מאיכות נמוכה מהפלסטיק המקורי. לאחר תהליך מיחזור נוסף או שניים כבר אי אפשר להשתמש בחומר הגלם. כמו בסיפור המולקולות במיכל, גם כאן מדובר בפגיעה במבנים המיקרוסקופיים בצורה שלא ניתנת לתיקון. אך עדיין אין ניסוח לחוק דומה לגבי חומר.

אנטרופיה וחיים

אם נביט על כדור הארץ בארבע מיליארד השנים האחרונות ניראה דווקא את ההפך מהתחזית הפסימית של התרמודינמיקה: במקום התפוררות ושחיקה לכלל 'שיווי משקל תרמודינמי' אנחנו רואים שמהאוקיינוס החדגוני הקדום אט אט התפתחו להם יצורים חיים בעלי מורכבות הולכת וגדלה, ואקו-סיסטמות נוצרו ובהן יחסי גומלין מורכבים. כל אלה, כך נדמה, סותרים את החוק השני של התרמודינמיקה.

ובכן, ההתפתחות הביולוגית סותרת את 'רוח' החוק, אך לא את לשונו. כזכור, החוק השני תקף לגבי מערכות סגורות, ואילו כדור הארץ הוא מערכת פתוחה המחליפה אנרגיה עם סביבתה. כך יכולות המערכות הביולוגיות לנצל אנרגיה זו כדי ליצור תחומים סגורים (אורגניזמים) בהם הסדר עולה. יש לזכור שיצורים חיים צורכים כל הזמן אנרגיה וחומרים בעלי אנטרופיה נמוכה, ופולטים פסולת בעלת אנטרופיה גבוהה.

הערות של שחר

לגבי הקרינה מהשמש, כמות האנרגיה הנקלטת והנפלטת שוות (פחות או יותר, כל עוד כדור הארץ לא מתחמם או מתקרר). אך האנטרופיה שונה: כדור הארץ מקבל קרינה באנטרופיה נמוכה מהשמש ופולט קרינה באנטרופיה גבוהה הרבה יותר – כך שהוא מייצא אנטרופיה לחלל. יש לשים לב שגם ללא יצורים חיים תהליך זה היה מתרחש!
כזכור, החוק השני של התרמודינמיקה מבוסס על חוסר הידע וחוסר היכולת שלנו לטפל בסקאלה של אטומים בודדים. אך המערכות החיות עושות בדיוק את זה: החלבונים מהווים מכונות ננו מטריות בעלות יכולת זיהוי ופעולה ברמה האטומית. יכולת זו היא המאפשרת למערכת ביולוגית להיות מעגלית: אורגניזמים מסוג אחד מסוגלים לפרק את הפסולת של אורגניזמים מסוג אחר ולהשתמש בה כמזון. כך נשמרת האקו-סיסטם במצב של אנטרופיה נמוכה. אך יש לזכור שכל זה נעשה אך ורק בזכות שטף מתמיד של אנרגיה המגיע מהשמש. בלעדיו האנטרופיה על כדור הארץ לא הייתה מצליחה לרדת במהלך האבולוציה.

אנטרופיה וכלכלה

הפרוייקט הנאו-ליברלי התבסס על הפיכת הכלכלה למדע מדוייק. בהסתמכם על מדדים כמותיים כגון סחורות, שרותים וכסף, יכלו הכלכלנים לפתח תיאוריות עקביות המבוססות על אקסיומות, ממש בדמות המכניקה. אך בעוד המכניקה עסקה בתהליכים הפיכים ודטרמיניסטים, הכלכלה עוסקת בתהליכים חברתיים מורכבים שהם בלתי הפיכים ואינם ניתנים לחיזוי. בתהליכים כאלו החוק השני נכנס לפעולה ויוצר א-סימטריה בזמן.

בניגוד לתרשים המעגלי של הכלכלנים, הייצור התעשייתי מתבסס על אספקה שוטפת של חומרי גלם ואנרגיה מהביוספרה, ופולט פסולת גבוהת אנטרופיה חזרה.

כך שהכלכלה תלויה ביכולת הסביבה לספק חומרי גלם ואנרגיה ולקלוט חזרה את הפסולת.

מושגים נוספים

כעת, נעשה מספר הבחנות בין סוגים שונים של משאבים במחסור, הבחנות שהכלכלנים הנאו-קלאסיים לא עושים (או עושים, אך מתייחסים אליהן כמשניות) והן מהותיות לניתוח השימוש במשאבים. החשיבות גדולה כשדנים בייצור האנושי, אך חשוב מכך, כאשר דנים בשירותים והטובין הניתנים על ידי הסביבה.

מאגרים (Stock flow)

חומר הגלם שהופך להיות חלק מהמוצר עצמו (במינוח האריסטוטלי: הסיבה החומרית). בייצור לחם, למשל, אלו הקמח והמים.

ניתן לאגירה (Stock)
ניתן להשתמש באיזה קצב שרוצים (Flow)
הפיריון נמדד במספר יחידות מוצר
נצרך בתהליך הייצור

זרמים/שירותים (Fund service)

המערכות שמאפשרות את הייצור (הסיבה הפועלת), אך לא הופכות להיות חלק מהמוצר. בייצור לחם, אלו הטבח והתנור.

ניתנים לשימוש בקצב מסויים בלבד
הפיריון נמדד בקצב ייצור
לא ניתן לאגירה (הטבח לא יכול 'לאגור' את יכולת הייצור מספר ימים, ולבצע אותה בקצב כפול לאחר מכן...)
הקרן (Fund) לא נצרכת בתהליך הייצור, אך יכולה להישחק.

בלבדיות (Excludability)

מושג משפטי המציין שיש אפשרות חברתית לאפשר גישה בלבדית למשאב מסוים. למשל, בחברה המודרנית אני יכול להיות הבעלים של אופניים ובכך למנוע מכל אחד אחר שימוש בהם (אפילו כשאני לא משתמש בהם). פנס רחוב, מאידך, יכול להיות בבעלותי, אך קשה מאוד למנוע מעוברי האורח להשתמש בשרותיו.

יריביות (Rivalness)

תכונה פנימית של משאב המציינת ששימוש בו מצמצם את האפשרות של אחרים להשתמש בו. כשאני נוסע באופניים, אחרים לא יכולים לעשות זאת, אך כשאני משתמש בשכבת האוזון כמגן מקרינת UV אני לא מונע מאחרים לעשות זאת גם. ניתן לפגוע בשכבת האוזון, אך זה לא נעשה דרך השימוש בה.

כל המאגרים הם יריביים שכן שימוש במאגר כמו קמח או מים על ידי אדם אחד, מונע את השימוש בו על ידי אדם אחר. כל הטובין שאינם יריביים הם זרמים. אך לעיתים זרם/שרות הוא בלבדי (אופניים לדוגמה).

סוכם על ידי שחר דולב